Mācību materiāls
8. Dinamikas statistiskā izpēte
8.3. Dinamikas rindas izmaiņu tendences metodes
Svarīgs sociālekonomisko procesu likumsakarību pētīšanas virziens ir dinamikas rindas kopējās attīstības tendences – trenda noteikšana. Pētāmo objektu dinamikas rindu līmeņi svārstās – gan palielinās, gan samazinās. Šādos gadījumos, lai noteiktu trendu, lieto īpašas dinamikas rindu izlīdzināšanas metodes.
Trenda izzināšana nepieciešama lai pilnīgāk noskaidrotu pētāmās parādības attīstības raksturu, kāds faktiski bijis jau aizritējušā periodā, kā arī lai iegūtu teorētiski pamatotu bāzi dinamikas rindas turpināšanai, t.i., parādības prognozēšanai.
Trenda noteikšanai lieto speciālas metodes. Visplašāk lieto intervālu paplašināšanas, slīdošo vidējo un analītiskās izlīdzināšanas metodi.
Intervālu paplašināšanas metode saistīta ar sākotnējās dinamikas rindas pārveidošanu ilgstošāku periodu rindās (piemēram, dienas – mēneša, mēneša – ceturkšņa, ceturkšņa – gada u.t.t.). Šī metode ir pārāk elementāra. To var lietot tad, ja rinda, kuru pārveido, ir pietiekami gara.
Slīdošo vidējo metode. Arī šīs metodes pamatā ir intervālu paplašināšanas princips. Veidojot katru jaunu paplašinātu intervālu, tā sākuma punkts "paslīd" par vienu laika vienību uz priekšu. Šī metode piemērota tajos gadījumos, kad parādības attīstībai ir nevienmērīgs raksturs. Tā ļauj atbrīvoties no sezonālās ietekmes.
Analītiskā izlīdzināšanas metode ir visefektīvākā trenda atklāšanas metode. Tā ne tikai atklāj trendu, bet arī palīdz analizēt dinamikas rindu savstarpējo sakarību (korelāciju).
Dinamikas rindas analītiskā izlīdzināšana nozīmē, ka faktiskie dinamikas rindas līmeņi ![]() tiek aizvietoti ar teorētiskiem līmeņi
tiek aizvietoti ar teorētiskiem līmeņi ![]() . Ja faktiskos dinamikas rindas līmeņus attēlo grafiski, iegūst lauztu līniju, kas atspoguļo gan galveno tendenci, gan arī dažādas novirzes, kas radušās vai nu sezonas svārstību, vai citu faktoru rezultātā. Lai noskaidrotu galveno – pamattendenci, iztaisnošanu var veikt gan pēc taisnes, gan pēc kādas citas līnijas, kas atspoguļo dinamikas rindas līmeņu funkcionālo atkarību no laika. Atsevišķas funkcijas izvēles pamatā ir parādības būtības teorētiskā analīze un attīstības parādību likumi. Atkarībā no parādības attīstības tipa lieto noteiktu matemātiskās funkcijas veidu. Visbiežāk analītiskā izlīdzināšana notiek atbilstoši taisnes vienādojumam.
. Ja faktiskos dinamikas rindas līmeņus attēlo grafiski, iegūst lauztu līniju, kas atspoguļo gan galveno tendenci, gan arī dažādas novirzes, kas radušās vai nu sezonas svārstību, vai citu faktoru rezultātā. Lai noskaidrotu galveno – pamattendenci, iztaisnošanu var veikt gan pēc taisnes, gan pēc kādas citas līnijas, kas atspoguļo dinamikas rindas līmeņu funkcionālo atkarību no laika. Atsevišķas funkcijas izvēles pamatā ir parādības būtības teorētiskā analīze un attīstības parādību likumi. Atkarībā no parādības attīstības tipa lieto noteiktu matemātiskās funkcijas veidu. Visbiežāk analītiskā izlīdzināšana notiek atbilstoši taisnes vienādojumam.
Ja pētāmai parādībai ir vienmērīgs attīstības raksturs: ![]() ; kur
; kur ![]() izlīdzinātās rindas līmeņi, kurus vajag aprēķināt;
izlīdzinātās rindas līmeņi, kurus vajag aprēķināt; ![]() taisnes parametri;
taisnes parametri; ![]() laika rādītāji (dienas, mēneši u.t.t.).
laika rādītāji (dienas, mēneši u.t.t.).
Ja parādībai ir pakāpeniski paātrināts, augošs raksturs, izlīdzināšanu var izdarīt atbilstoši parabolas vienādojumiem.
Lai aprēķinātu izlīdzināšanai izraudzītās analītiskā vienādojuma konstantes ![]() un
un ![]() , jāsastāda un jāatrisina normālvienādojuma sistēmā:
, jāsastāda un jāatrisina normālvienādojuma sistēmā: 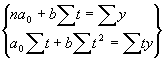 ; kur
; kur ![]() rindas locekļu skaits;
rindas locekļu skaits; ![]() laika periodi;
laika periodi; ![]() dinamikas rindas sākotnējie līmeņi.
dinamikas rindas sākotnējie līmeņi.
