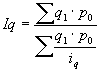Mācību materiāls
| Vietne: | E-studijas |
| Kurss: | STAT001 Ievads statistikā |
| Grāmata: | Mācību materiāls |
| Drukājis: | Vieslietotājs |
| Datums: | Sunday, 2025. gada 19. October, 16:03 |
Satura rādītājs
1. Statistikas priekšmets
“Statistika – māksla sniegt precīzus datus par to, ko zini” – rakstīja
Francijas valstsvīrs un vēsturnieks Ādolfs.Tjers (Marie Joseph Louis Adolphe
Thiers, 1797-1877). Zināt statistiku, tas ir stils. Mode var mainīties, bet stils paliek.
Atverot studiju kurus materiālu, Tu vispirms iepazīsies ar statistikas vēsturi, statisku kā zinātni, kas ir statistikas teorētiskais pamats, un, kādi ir statistikas uzdevumi.
Statistikas vēsture
Cilvēcei tās attīstības gaitā ir bijusi nepieciešamība ievākt datus un saprast, ko tie izsaka. Senajā Ēģiptē, Grieķijā, Romas impērijā dati tika ievākti, galvenokārt, lai varētu iekasēt nodokļus, zināt iedzīvotāju skaitu, īpašumus un zemi, veikt militārās operācijas. Viduslaikos baznīca bija tā, kura reģistrēja jaunpiedzimušos, mirušos un laulības. Attīstoties valstu tautsaimniecībām valsts pārvaldei un pilsoniskai sabiedrībai būtiski bija zināt, kas notiek preču realizācijas tirgos, kur un cik daudz iegūt izejvielas, uzskaitīt ražošanas spēku.
Nepieciešamība pēc uzskaites dažādās valstīs veicināja statistikas kā zinātnes veidošanos. Statistika kā zinātne sāka attīstīties 17. gs. vidū divos virzienos:
- aprakstošā;
- matemātiskā.
Izpratne par aprakstošo statistiku sāka veidoties Vācijā 17.gs. sākumā. Šīs skolas ievērojamākie pārstāvji ir G. Konrings (1606.-1681.) un G. Ahenvals (1719.-1772.), kurš pirmoreiz Marburgas universitātē 1746. g. uzsāk lasīt lekcijas jaunā disciplīnā, kuru nosauc par statistiku.
Interesanti, ka aprakstošās skolas pārstāvji vispār izvairījās no skaitlisko datu izmantošanas un tikai vēlāk (18.gs. vidū) skaitliskie dati pakāpeniski iekaro tiesības tikt ietvertiem aprakstošās statistikas darbos.
Statistika ir cieši saistīta ar matemātiku. Matemātiskais virziens
statistikā sāka veidoties Anglijā ap 17. gs. sākumā, saucoties kā
politiskā aritmētika.
Šī virziena pamatlicējs un spilgtākais pārstāvis ir V.Pettijs (1623.-1742.). Atšķirībā no aprakstošās skolas matemātiskā virziena pārstāvji par savu uzdevumu izvirzīja ekonomisko parādību likumsakarību un savstarpējo sakarību atklāšanu ar dažādu aprēķinu palīdzību.Tās uzdevums, ekonomisko un demogrāfisko datu
apkalpošana.
Ap 1800. g., izmantojot varbūtības teoriju, izveidojas statistiski matemātiskais virziens, kā "sociālā fizika". Īpašu ieguldījumu šī virziena attīstībā deva beļģu statistiķis A. Ketlē (1796.-1874.). Lielu ieguldījumu varbūtību teorijas attīstībā, kas veido vienu no statistikas nozarēm deva B. Paskals (1623.-1662.), J. Bernulli (1667.-1748.), spēļu teorija, binārais sadalījums un K. Gauss (1777.-1855.), normālais sadalījums, t.s. "Gausa līkne".
Statistikas zinātne
Literatūrā ir atrodamas daudz termina "statistika" definīcijas. Vienkāršākā no tām ir šāda.
Statistika ir zinātne par datu savākšanu, attēlošanu un analīzi.
Termins statistika – cēlies no latīņu valodas vārda "status", kas nozīmē – stāvoklis. Zinātnes un tehnoloģijas vārdnīcā ir rakstīts.
Statistika ir zinātnes nozare, kurā pēta cilvēku sabiedrības, dabas parādību u.c. kvantitatīvās pārmaiņas; statistisko datu savākšana, analīze un interpretācija.
- Zināt, kā pareizi reprezentēt un aprakstīt informāciju.
- Zināt, kā veikt secinājumus par ģenerālo kopu (vispārināšana), balstoties uz informāciju par izlasi.
- Zināt, kā veidot un uzlabot procesus (t.sk. biznesa).
- Zināt, kā iegūt ticamu prognozi.
Savukārt, svešvārdu vārdnīca terminu statistika skaidro šādi:
- Zinātņu nozare, kas kvantitatīvi pētī cilvēku sabiedrības un dabas parādības.
- Datu kopums par kādu parādību vai procesu.
- Matemātiskā statistika – lietišķās matemātikas nozare, kas pētī ,kā pareizi iegūstami dati un kā tie pareizi apstrādājami, izstrādā nepieciešamos matemātiskos modeļus.
Statistika ir zinātne, kas nodarbojas ar sabiedrisko parādību stāvokļa un pārmaiņu skaitlisku uztveršanu un mērīšanu un pētī sabiedrisko parādību un procesu skaitliskās likumsakarības konkrētos vietas un laika apstākļos.
Statistikas pētījumu priekšmets ir sociāli ekonomiskās dzīves masveida parādības. Tā pēta šo parādību kvantitatīvo pusi ciešā saistībā ar kvalitatīvo saturu konkrētos vietas apstākļos un laikā.
Statistikas teorētiskais pamats
Kā jebkurā zinātnē, t.sk. ari statistikā teorētisko pamatu veido jēdzieni un kategorijas, kuri kopumā definē attiecīgās zinātnes galvenos principus.
Statistikā svarīgākie jēdzieni un kategorijas ir šādi:
- kopa;
- pazīme;
- variācija;
- likumsakarība.
Parādības kopuma pētīšana pēc vienas vai vairākām pazīmēm, kas pastāv ierobežoti laikā un telpā, saucas statistiskā kopa.
Piemērs. Dažādu produkcijas veidu ražošana, patēriņš, produkcijas eksports un imports. Šajā gadījumā ir runa par masveida parādību, kas sastopama lielā skaitā, kas ir jāizpēta, izmantojot parādības statistisko kopu. Praktiski un bieži praksē tiek izmantotas mazas kopas, kas saucas izlases.
Statistiskajai kopai piemīt:
- masveidīgums – liels skaits individuālu gadījumu;
- vienveidīgums;
- skaitliska izpausme;
- regularitāte, atkārtošanās.
Sabiedriskās parādības ir konkrētas un reālas, tātad izmērāmas.
Statistiskā kopa (jeb kopas vienība) sastāv no elementiem. Katru elementu raksturo tam piemītošās pazīmes.
Piemērs. Uzņēmuma darbinieki, kuriem ir kopīgas īpašības jeb pazīmēs.
Pazīmes pēc izteiksmes veida iedala:
1. Kvantitatīvās (skaitliski izteiktas).
Piemērs. Darba samaksa, nostrādās stundas.
2. Kvalitatīvās (vārdiski izteiktas).
Piemērs. Ieņemamais amats.
Statistiskajā kopā pazīmēm eksistē arī variācijas jeb skaitliskas atšķirības.
Statistiskais rādītājs ir pētāmās parādības skaitliskais vērtējums, kas ietver sevī gan kvalitatīvo, gan kvantitatīvo pusi. Tipisku kopas vienības īpašību mēra ar vidējiem rādītājiem (aprakstošā statistika).
Pastāv statistiskās kopas vienveidīguma jēdziens, ar ko saprot kopas visām vienībām piemītošās galvenās īpašības. Viena un tā pati kopa var būt vienveidīga pēc vienas pazīmes un nevienveidīga pēc citas.
Pazīmes kvantitatīvā vai kvalitatīvā izmaiņa, pārejot no kopas vienas vienības uz citu saucas variācija.
Par statistisko likumsakarību pieņemts saukt atkārtošanos, secību un izmaiņu raksturu parādībās.
Statistiskās informācijas lietošana uzņēmumā palīdz atrisināt ne vienu vien problēmu, taču būtiski izprast skaitļu valodu. Tāpēc svarīgi iepazīties ar statistikas metodoloģiju: kopēju noteikumu, statistisko pētījumu paņēmienu sistēmu, kas nodrošina sociāli ekonomisko procesu struktūras, dinamikas, savstarpējo sakarību skaitlisko likumsakarību izpēti.
Statistikas metodoloģijas pamats ir izziņas teorija, t.i. dabas un sabiedrības izpēte savstarpējā iedarbībā, saistībā, dinamikā un attīstībā.
Statistisko pētījumu process izpaužas statistiskās pētīšanas trīs etapos:
- Sākotnējās informācijas apkopošana (materiāla grupēšana un sakopošana).
- Sākotnējās statistiskās informācijas savākšana (statistiskā novērošana).
- Statistisko rādītāju apstrāde, analīze un interpretācija (skaidrojums).
Statistiskos pētījumus raksturo struktūru, sadalījumu.
Piemērs. Viesnīcu ienākumi pa viesnīcu lieluma grupām. nevis "visas viesnīcas kopā".
Statistika pēta arī sakarības (cēloņi un sekas, dinamiskas, teritoriālas sakarības u.tml.).
- pētījuma mērķis (neiespējami "savākt visu");
- pētījuma plānošana (ievērojot apstrādes metodi);
- datu un/vai informācijas ievākšana (aptaujas anketas, intervijas, monitorings u.c.);
- datu un/vai informācijas apstrāde (sistematizācija, klasifikācija, grupu veidošana);
- datu kopas analīze;
- datu attēlošana (tabulas, grafiki u.tml.);
- interpretācija (hipotēžu pārbaude, salīdzinājumi ar citiem datiem);
- secinājumi un priekšlikumi.
Statistikas uzdevumi
Valsts statistikas galvenie uzdevumi ir:
- apkopot un analizēt savākto statistisko informāciju;
- publicēt šo informāciju, darot to pieejamu visai sabiedrībai;
- veidot vienotu, uz starptautiski atzītiem metodoloģijas principiem pamatotu, statistiskās informācijas sistēmu;
- veidot viedu statistiskās informācijas sistēmu, optimālu lēmumu pieņemšanai visa līmeņa institūcijām, kā arī pētījumu un domu apmaiņas veicināšanai.
Valsts statistikas darbu mūsu valstī vada LR Centrālā statistikas
pārvalde (CSP): http://www.csb.gov.lv - tiešās pārvaldes iestāde, kura ir galvenā
valsts oficiālās statistikas darbu veicēja un koordinatore. Valsts statistikas
galvenie uzdevumi noteikti likumā "Valsts statistikas likums". Valsts statistikas likums (VSL) nosaka valsts statistikas darba
organizācijas kārtību Latvijas Republikā (LR Saeimā
pieņemts 06.11.1997.): http://www.likumi.lv
Valsts statistikas galvenie uzdevumi ir šādi (likums "Valsts statistikas likums" 3 pants (1)):
- veidot vienotu, uz starptautiski atzītiem metodoloģijas principiem pamatotu statistiskās informācijas sistēmu par sabiedrībā notiekošajām ekonomiskajām, demogrāfiskajām un sociālajām parādībām un procesiem, kā arī vidi;
- apkopot un analizēt savākto statistisko informāciju;
- publicēt šo informāciju, darot to pieejamu visai sabiedrībai;
- sniegt Saeimai, valsts institūcijām un plašākai sabiedrībai statistisko informāciju, kas nepieciešama lēmumu pieņemšanai, kā arī pētījumu un domu apmaiņas veicināšanai.
Eiropas statistikā informācija tiek publicēta: http://ec.europa.eu/eurostat
2. Statistiskā novērošana
Datu vākšana, sistematizācija, analīze un interpretācija ir būtiska daudzos ar biznesu saistītos procesos. 2.nod. uzzināsi, ka statistika dalās, - aprakstošā un izskaidrojošā statistikā, kādi ir datu tipi, un, kas ir statistiskā novērošana.
Aprakstošā un izskaidrojošā statistika
Statiska dalās divās daļās.
1. Aprakstošā statistika.
2. Izskaidrojošā statistika.
Aprakstošā statistika ietver datu kopas datu ievākšanas, prezentēšanas un analīzes metodes, nolūkā ticami un patiesi aprakstīt datu kopu.
Izskaidrojošā statistika ietver datu metodes, lai prognozētu ģenerālās kopas raksturlielumus, balstoties tikai uz izlases datiem.
Dati (lat.datum) datu bāzē ierakstīts faktu kopums.
Informācija (lat. informatio) interpretēti un cilvēkam saprotamā veidā pasniegti dati.
Datiem pašiem par sevi nav būtiskas vērtības, vērtība ir informācijai ko iegūst no datiem.
Datu formas ir:- simboli (cipari, burti);
- attēli;
- audio;
- video.
Datu tipi
Atribūti un vērtības
Jebkuru datu kopu var apskatīt kā datu objektu sakopojumu. Datu objektu var nosaukt arī par piemēru vai ierakstu, un tās galvenās pazīmes tiek aprakstītas ar atribūtiem.
Piemērs. Notikuma ilgums, fiziska objekta svars.
2.1. tabula. Dažādi atribūtu tipi.
|
Atribūta tips |
Apraksts |
Piemēri |
Operācijas |
|
|
Kategoriskie |
Nomināls |
Vērtības ir vienkārši apzīmējumi, satur tikai tik daudz informācijas, lai atšķirtu vienu objektu no cita ( =, ≠). |
Objekta krāsa, automobiļa modelis, pasta indekss. |
Moda. |
|
Kārtas |
Kārtas atribūtu vērtības satur pietiekamu informāciju, lai sakārtotu objektus (<, >). |
Māju numuri, vietas kinoteātrī , studenta ID. |
Mediāna. |
|
|
Skaitliskie |
Intervāla |
Intervāla atribūtiem atšķirībai starp vērtībām ir jēga, t.i., pastāv mērvienība (+, -). |
Studenta reitings, kalendāra dati, ģeogrāfiskās koordinātes. |
Vidējais aritmētiskais, standartnovirze. |
|
Proporcijas |
Proporcijas atribūtiem ir svarīgi ne tikai starpība starp vērtībām, bet arī proporcionālās sakarības (*, /). |
Vecums, svars, augums. |
Ģeometriskais vidējais, harmoniskais vidējais |
|
Statistiskā novērošana
Statistiskā novērošana ir statistiskās pētīšanas pirmais posms.
Statistiskā novērošana ir sistemātiska, plānveidīga un racionāli organizēta, uz statistikas zinātnes un prakses atziņām balstīta sākotnējās datu vai informācijas vākšana par sabiedriskajām parādībām un procesiem, lai to varētu izlietot statistiskai vispārināšanai un analīzei.
Statistiskā novērošana palīdz reaģēt uz tirgus izmaiņām, pareizi organizēt mārketinga stratēģiju, novērtēt un organizēt biznesa procesus u.tml.
Novērošanas mērķis ir iegūt ticamu datus vai informāciju par vienas vai otras sociāli ekonomiskās parādības stāvokli vai procesa raksturu. Novērošanas rezultātā iegūst plašu individuālu faktu materiālu, pēc kura vēl nevar spriest par pētāmo parādību likumsakarībām un pieņemt optimālus lēmumus.
Iegūtajiem datiem jābūt:
- Ticamiem – jāatbilst reālajai patiesībai.
- Pilnīgiem, t.i. jāaptver visas statistiskās kopas vienības, ja tas nav iespējams, jāveido pamatota izlase.
- Savlaicīgiem un lētiem.
- Vienveidīgiem un salīdzināmiem.
Statistisko novērojumu veikšanai jārisina organizatoriskie jautājumi, kas ir šādi:
Novērošanas programmas izstrāde - jautājumu loks, uz kuriem jāsaņem atbildes - jāietver būtiskās pazīmes, jautājumi jāveido precīzi, nepārprotami, jāizkārto loģiskā secībā, jāietver kontroles jautājumi, jāizveido formulārs (aptaujas veidlapa, anketa, uzskaites karte u.c.) un instrukcija;
- Jānosaka novērošanas institūcija.
- Novērošanas laiks un vieta, kā arī jānorāda laiks, kurā jāapstrādā iegūtie dati.
- Jāsastāda atskaites vienību saraksts.
- Novērošanas materiālu un kopsavilkumu nodošanas un saņemšanas kārtība.
- Jāveic speciālistu apmācība.
- Darbs ar presi, medijiem.
- Kļūdu labošana.
- Izmaksu tāmes izstrāde u.c.
Novērošanas sagatavošanas posmā precīzi jānosaka novērošanas objekts: pētāmā statistiskā kopa, kurā notiek sociāli ekonomiskās parādības un procesi.
Piemērs. Banka, uzņēmumi, nodarbinātie, studējošie.
Pētāmais objekts sastāv no novērošanas vienībām:objekta pamatelementa, kura būtiskākās pazīmes novērošanas procesā reģistrē.
Piemērs. Darbinieks, studējošais.
Novērošanas pazīmes ir īpašības, kas piemīt novērojamajai vienībai. Pēc novērošanas vienībām piemītošajām īpašībām, pazīmes var iedalīt:
- Kvalitatīvas (atributīvās) pazīmes.
- Kvantitatīvās (skaitliskas) pazīmēs, kuras var izteikt ar skaitļiem.
Kvantitatīvās pazīmes var būt:
1. diskrētās (pārtrauktās), kuras izsaka veseli skaitļi;
Piemērs. Cilvēku skaits ģimenē, istabu skaits dzīvoklī.
Šādos gadījumos variantus nodala mērīšanas vai reģistrācijas precizitāte.
2. nepārtrauktās, kuru izteiksmes forma var būt kā veseli skaitļi tā arī daļas.
Izšķir vairākus novērošanas veidus.
1. Pēc pētāmā objekta pilnīguma:
- pilnā novērošana, kad tiek novērotas visas novērošanas vienības;
- nepilnā novērošana, kuru izmanto, ja novēro tikai kopas daļu vai arī veic izlases novērošanu, kas ir zinātniski visvairāk pamatota.
2. Pēc informācijas ieguves regularitātes: nepārtrauktā, vienreizējā, periodiskā.
3. Pēc ziņu ieguves veida: pārskati un speciāli organizētas statistiskās novērošanas.
Novērošanas organizatoriskās formas ir pārskati un speciāli organizētas statistiskās novērošanas, kā arī reģistri. Galvenā ir statistiskie pārskati.
Novērošanas vieta - teritoriāli administratīvā vieta, kurā par katru vienību tiek reģistrētas ziņas. Novērošanas laiks - kalendārais laiks, gads, gadalaiks, ceturksnis, mēnesis, kad notiek statistiskā novērošana.
Statistiskās novērošanas galvenais uzdevums ir iegūt patiesu, precīzu, ticamu informāciju. Tomēr novērošanas gaitā neizbēgama ir kļūdu rašanās. Tāpēc jāveic materiālu kontrole, un, ja nepieciešams, kļūdas jālabo. Kļūdu novēršanai lieto loģisko un aritmētisko kontroli.
3. Statistiskie dati kā analīzes objekts
Šajā nodaļā Tu iepazīsies ar statistisko datu grupēšanu, ka statistikā ir sadalījuma rindas, kā arī ar statistiskām tabulām un grafikiem.3.1. Statistisko datu grupēšana
Par grupēšanu sauc statistiskā kopuma sadalīšanu pēc kopējām īpašām pazīmēm kvalitatīvi viendabīgās daļās jeb grupās.
Statistiskā grupēšana ir statistisko kopu veidošana pēc kopējām īpašām pazīmēm, t.i., datu apkopojuma un analīzes metode un tā balstās uz analīzi un sintēzi.
Atkarībā no konkrētā pētījuma uzdevumiem, jārisina grupēšanas metodoloģiskās problēmas:
1. grupēšanas uzdevuma formulēšana;2. grupēšanas pazīmes vai to kombināciju izvēle;
3. grupu skaita un grupu intervālu garuma noteikšana;
4. grupu raksturojošo rādītāju noteikšana;
5. sakopošanas tehniskā īstenošana.
Grupēšanas rezultātus atspoguļo tabulās (starpsummu tabulas, šķērsgriezumu tabulas u.c.).
Grupēšanas uzdevumi:
- parādību sociāli ekonomisko tipu veidošana;
Piemērs. Uzņēmumu grupēšana pēc īpašumu formām, viesnīcu grupēšana pēc ienākumiem.
- parādību struktūras un tās izmaiņu izpēte;
- sakarību atklāšana starp pētāmajām parādībām.
Grupu veidošana princips balstās uz nepieciešamās grupēšanas pazīmes izvēles, kura pēc sava rakstura var būt:
1. Kvalitatīva. Skaitliskas: diskrētas (objektu skaits), nepārtrauktas (naudas summas, objektu vērtība, svars u.c.).
Piemērs. Darbinieki pēc to izglītības, dzimuma.
Grupu skaitu šādos gadījumos ietekmē pazīmes kvalitatīvais raksturs.
Ja kvalitatīvai pazīmei ir daudz veidu, tad par pamatu var kalpot klasifikācija, ko nosaka standarti vai pētījuma mērķis.
Klasifikators ir sistematizēts kopas elementu, vienību saraksts, viens no svarīgākajiem dokumentiem datu automatizēto sistēmu projektēšanā;
2. Kvantitatīva. Atributīva (vārdiska izteiksme). Kvantitatīvie grupējumi var būt ļoti dažādi un var veidot daudz grupas. Grupu skaitu nosaka pētāmā rādītāja variācija.
Primārais grupējums - grupējums, kuru veic pirmo reizi. To pazīmi, pēc kuras grupē, sauc par grupējuma pamatu.
Ja grupas izveido pēc vienas pazīmes, tad tādu grupējumu sauc par vienkāršu grupējumu. Ja grupas izveido vienlaicīgi pēc divām vai vairāk pazīmēm, tās savstarpēji saistot un kombinējot, tad tādu grupējumu sauc par kombinētu grupējumu. Gadījumos, kad grupēšanas pazīme ir ar plašām robežām, veido intervālus.
Intervāls ir pazīmes nozīmes, kas atrodas noteiktās robežās. Praksē lieto vienāda un nevienāda garuma intervālus. Vienāda garuma intervālus izmanto tajos gadījumos, kad pazīme zināmās robežās mainās vienmērīgi.
Piemērs. Vienas profesijas darbinieku grupējums pēc darba samaksas lieluma.
Nevienāda garuma intervālus izmanto tad, kad katra grupa rāda noteiktu tipu.
Piemērs. Bērnu skaits pirmsskolas vecumā, sākumskolas, pamatskolas un vidusskolas vecumā u.tml.
Nevienāda garuma intervālus visbiežāk lieto analītiskos grupējumos.
Sekundārais grupējums. Otrreizējais grupējums, kuru veic pilnībā vai daļēji pārveidojot iepriekšējo grupējumu vai tikai kādu tā daļu. Saistot grupēšanu ar tai izvirzītajiem uzdevumiem, izdala šādus grupēšanas veidus:
1. Tipoloģiskā grupēšana - pētāmas kopas sadalīšana kvalitatīvi vienveidīgās grupās.
2. Struktūras grupēšana tiek veikta kvalitatīvi viendabīgas kopas struktūras izpēte.
Piemērs. Lai analizētu nodarbināto sastāva izmaiņu pa profesijām.
3. Analītiskās grupēšanas uzdevums ir atklāt un raksturot sakarības starp dažādām pazīmēm, no kurām vienu uzskata kā rezultātu, bet citas kā faktorus. Pazīmes izvieto noteiktā secībā, ievērojot iespējamo sakarību loģiku.
3.2. Sadalījuma rindas
Par statistiskajām rindām sauc statistiskās kopas elementu sadalījumu pēc kādas skaitliskas vai atributīvas variējošas pazīmes jeb datu objekta raksturojošās īpašības, ko sauc par atribūtu vai mainīgo lielumu. Rinda var variēt kā izmaiņas telpā, laikā, vai arī atkarībā no citu pazīmju izmaiņām.
Statistiskās empīriskās rindas piemērs.
Dots. Uzņēmuma labiekārtošanas darbos nodarbināto skaits pa dienām.
Definēsim, ka tas ir atribūts "nodarbinātība". Dati doti datu kopas veidā, sk. 3.2.1. tabulu.
3.2.1.tabula. Nesakārtota statistiskā kopa.
| 1 | 5 | 7 | 2 | 1 |
| 6 | 4 | 4 | 3 | 9 |
| 6 | 6 | 8 | 1 | 6 |
| 8 | 3 | 4 | 9 | 1 |
| 3 | 8 | 5 | 7 | 1 |
Piemērā redzamā datu kopa nav sakārtota. Nesakārtoto novērojumu rindu apstrādā, iegūstot sakārtotu sadalījuma rindu jeb variāciju rinda.
Sadalījuma rindas, kuras sakārtotas pēc kvantitatīvām pazīmēm sauc par variācijas rindām.
Variāciju rinda ir statistiskās kopas vienību sadalījums pēc kādas skaitliski vai atributīvi variējošas pazīmes.
Statistiskās kopas sakārtošanu statistikā sauc par ranžēšanu.
Ranžēšana ir datu vai informācijas sistematizēšana, tās sakārtošana kvantitatīvā vai kvalitatīvā nozīmīguma ziņā.
Informācijas sakārtošana tiek veikta vai nu:
- augošā kartībā jeb tiešais ranžējums;
- dilstošā kārtībā jeb ačgārnais ranžējums.
Atsaucoties uz doto piemēru, izveidojam sakārtotu empīrisko (pētniecisko) rindu. To veido, ranžējot sākotnējo informāciju augošā secībā, sk. 3.2.2. tabulu.
3.2.2.tabula. Augošā secībā ranžēta variācijas rinda.
| 1 | 1 | 1 | 1 | 1 |
| 2 | 3 | 3 | 3 | 4 |
| 4 | 4 | 5 | 5 | 6 |
| 6 | 6 | 6 | 7 | 7 |
| 8 | 8 | 8 | 9 | 9 |
Jebkuru sadalījuma rindu veido divi elementi:
![]() sadalījuma rindas variantes;
sadalījuma rindas variantes;
![]() varianšu biežums jeb frekvence.
varianšu biežums jeb frekvence.
Diskrētās sadalījuma rindas veido pārtraukti mainīgās pazīmes. Nepārtrauktu sadalījuma rindu veido lineāras taisnes vai līknes. Izveidojam tabulu, kurā norādām atribūta "nodarbinātība" augošā secībā ranēžetu sadalījuma rindu un tā frekvenci. Dotos datus mēs varam parādīt šādi, sk.3.2.3. tabula.
3.2.3.tabula. Ranžētas variāciju rinda frekvenču sadalījums.
|
|
|
| 1 | 5 |
| 2 | 1 |
| 3 | 3 |
| 4 | 3 |
| 5 | 2 |
| 6 | 4 |
| 7 | 2 |
| 8 | 3 |
| 9 | 2 |
Dienu skaits kopā: 25. No kurām visvairāk - 5 dienas, bija nodarbināts pa 1 cilvēkam.
Ja datu maz, tad variācijas rindu parasti nesastāda, bet aprēķina statistikas rādītājus tieši no nesakārtotas empīriskās rindas.
Atributīvās variāciju rindas ir pēc kvalitatīvās (vārdiskās) pazīmes veidots sadalījums.
Atributīvās rindas piemērs:
3.2.4.tabula. Iedzīvotāju sadalījums pēc dzimuma (skaits).
| Atribūts "dzimums" | uz 2016.g. sākumu |
| Vīrieši | 904 299 |
| Sievietes | 1 064 658 |
Variācijas rindas pēc pētāmās pazīmes rakstura iedalās:
- Diskrētās (pārtrauktās). Diskrētas variāciju rindas.
Piemērs. Studentu sekmju vērtējums ballēs: 3; 4; 5; 6; 7; 8; 9; 10;
- Nepārtrauktās (intervālu). Nepārtrauktās variāciju rindas veido pazīmes, kurām secīgi var būt jebkura skaitliska nozīme.
Diskrētās variāciju rindas, kurām ir daudz varianšu, apvieno grupās, veidojot intervālus.
Intervāls ir variējošas pazīmes nozīmes, kas atrodas noteiktās robežās.
Pastāv slēgti un atvērti intervāli.
Intervālu variāciju rindā variantes apvienotas plašākos intervālos (piem. no ... līdz....). Tās tiek iedalītas šādi:
- vienāda garuma intervālus, raksturojot kvantitatīvās pazīmes atšķirības vienādas kvalitātes grupu ietvaros;
- dažāda garuma intervālus lieto gadījumos, kad pazīmes nozīmes svārstības ir ļoti nevienmērīgas un ar plašu variāciju (analītiskie grupējumi).
Statistikā biežāk izmanto vienāda garuma intervālus.
Lai sastādītu sadalījuma rindu ar vienādiem intervāliem, vispirms jāatrod variācijas amplitūda. Kas ir starpība starp pazīmes maksimālo un minimālo nozīmi ![]() , tad intervāla garuma aprēķināšanai lieto formulu:
, tad intervāla garuma aprēķināšanai lieto formulu: ![]() , kur
, kur ![]() intervāla solis;
intervāla solis; ![]() maksimālā pazīmes vērtība;
maksimālā pazīmes vērtība; ![]() minimālā pazīmes vērtība;
minimālā pazīmes vērtība; ![]() grupu skaits. Vai arī izmanto Sterdžesa formulu:
grupu skaits. Vai arī izmanto Sterdžesa formulu: ![]() , kur
, kur ![]() visu novērojumu skaits.
visu novērojumu skaits.
Intervālus, kuriem dota tikai viena robeža (apakšējā vai augšējā ) sauc par atvērtiem vai nenoslēgtiem intervāliem.
3.3. Statistiskās tabulas
Statistiskās sakopošanas un grupēšanas, kā arī analīzes rezultātus parasti noformē statistiskajās tabulās. Galvenie tabulas elementi - tās priekšmets un izteicējs.
Tabulas priekšmets- ir to parādību vai parādību grupu nosaukums (uzskaitījums), ko raksturo tabulas rādītāji.
Tabulas izteicējs- rādītājs, kas raksturo tabulas priekšmetu.
Pēc priekšmeta rakstura tabulas iedala 3 grupās:
1. vienkāršās, kuru priekšmets ir novērošanas vienību vai objektu saraksts bez to grupējuma;
2. grupu, kuras priekšmets ir sadalīts pēc kādas vienas pazīmes;
3. kombinētās, kuru priekšmets ir kombinēts grupējums, kurā katra grupa ir sadalīta apakšgrupās pēc kādas citas pazīmes, t.i., grupējums tiek veikts pēc 2 vai vairāk pazīmēm.
3.4. Statistiskie grafiki
Statistiskie grafiki- ir rasējums, kurā ar dažādu ģeometrisku figūru palīdzību attēlo statistiskos datus. Ar attēlu palīdzību tiek raksturota kopas struktūra, skaidrāk un saprotamāk var uztvert pētāmās parādības attīstības tendenci, attēli paver plašas iespējas statistisko materiālu popularizēšanai. Attēli ir kā kontroles mehānisms, kuros var redzēt tabulās skaitļu rindās nepamanītās kļūdas.
Komercdarbības atspoguļošanai visbiežāk izmantojamie attēlu veidi (izmantoti nosacīti dati) ir:
1. Līniju diagrammas, kuras izvietotas koordinātu sistēmā. Izmanto ekonomisko procesu dinamikas raksturošanai.
3.4.1. att. Nominālais un realais IKP laika periodā no 2006. līdz 2016. gadam
2. Stabiņu diagrammas. Šajos gadījumos attēlojamos lielumus salīdzina pēc vienas dimensijas- līnijas vai stabiņa garuma (augstuma).
3.4.2. att. IKP faktiskās cenas un 2006.gada salīdzināmas cenas, EUR
3. Apļa diagrammas. Sadalot apļa laukumu proporcionālos sektoros, izveido sektoru diagrammu.
3.4.3.att. Uzņēmuma" W-Lat" pārdodo konfekšu procentālā frekvence no 2012. līdz 2016. gadam, procentos
4. Absolūtie un relatīvie lielumi
Statistiskie rādītāji kvantitatīvi raksturo statistiskās izpētes objektu. Statistiskiem rādītājiem jāatspoguļo pētāmās parādības būtība ar zināmu precizitāti, tāpēc skaitļus, kurus lieto statistika, nevar uzskatīt par abstraktiem.
4.1. Statistisko rādītāju veidi
Statistiskais rādītājs ir lielums, kas adekvāti raksturo pētāmo parādību konkrētas vietas un laika apstākļos. Lai iegūtu pilnīgu priekšstatu par pētāmo parādību, jāsaista tās kvalitatīvā un kvantitatīvā puse.
Statistiskajiem rādītājiem ir vairākas funkcijas, svarīgākās:
- izziņas (informatīvā);
- vadības (novērtēšanas);
- kontroles;
- prognozēšanas;
- reklāmas.
Pēc pētāmās parādības būtības, statistiskie rādītāji iedalās:
- kvantitātes rādītājos – izteikti mērvienībās, konkrēti skaitļi.
Piemēram: t, kg, skaits.
- kvalitātes rādītājos - konkrētu objektu īpašību rādītāji.
Kvantitatīvie rādītāji ir:
- visi ekonomiskie rādītāji. Piemēram: pašizmaksa, darba ražīgums, realizētā produkcija;
- demogrāfiskie (dzimstība, mirstība u.c.);
- makroekonomiskie (IKP, inflācija, bezdarbs);
- masveida parādību statistisko īpašību rādītāji.
Pēc teritoriālās noteiktības kvantitatīvie rādītāji var būt:
- reģionālie;
- vietējie.
Pēc pētāmās parādības izpētes pakāpes:
- individuālie rādītāji;
- kopsavilkuma rādītāji.
Pēc iegūšanas veida:
- apjoma rādītāji;
- aprēķina rādītāji.
Pēc pētāmās parādības rakstura:
- intervālu rādītāji, nosaka tad, ja tiem ir tendence pieaugt;
- momenta rādītāji, nosaka tad, ja tiem ir svārstīgu izmaiņu tendences.
Statistiskie rādītāji pēc izteiksmes formas iedalās:
- absolūtie lielumi;
- relatīvie lielumi;
- vidējie lielumi.
Statistiskie rādītāji pēc statistiskā rādītāja funkcijas:
- uzskaites rādītāji;
- novērtējuma rādītāji;
- analītiskie rādītāji.
4.2. Absolūtie lielumi
Par absolūtiem lielumiem statistikā sauc rādītājus, kas izsaka pētāmo objektu un parādību tiešos apjomus vai to veidojošo vienību skaitu.
Absolūtie lielumi izsaka konkrētu parādību apjomu, tāpēc tie vienmēr ir nosaukti lielumi un ir statistisko rādītāju pamatforma.
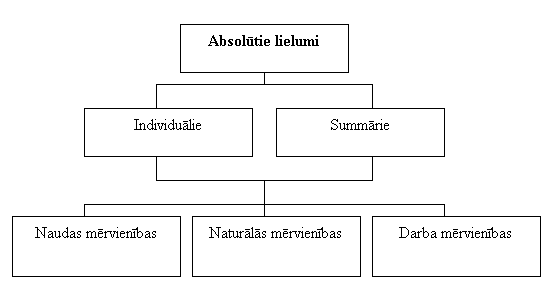
4.2.1.att. Absolūtie lielumi
Absolūto rādītāju izteikšanai lieto dažādas mērvienības, no kurām raskturīgākās ir:- naturālās:
- vienkāršās mērvienības;
- saliktās mērvienības.
- naudas;
- darba.
Summārie absolūtie lielumi ir individuālo lielumu apkopojums, kas izsaka vai nu visa pētāmā objekta, vai arī objekta kādas daļas lielumu.
Absolūtajiem lielumiem obligāti jābūt izteiktiem mērvienībās. Izšķir:
- naturālās – tonnas, kg, m2, gab., u.c.;
- naudas (vērtības)– lati, eiro, dolāri u.c.;
- darba – darba patēriņš cilvēkstundās, cilvēkdienās.
Sākotnējo informāciju var iegūt arī aprēķinu ceļā, izmantojot bilanču metodi.
Piemērs. Preču apgrozījumu veikalā mēnesī raksturo šāda informācija:
Preču atlikums mēneša sākumā - 124 000 EUR
+
Palielinājums mēneša laikā - 6000 EUR
-
Samazinājums mēneša laikā - 5000 EUR
=
Preču atlikums mēneša beigās - 125 000 EUR
Praksē lieto arī korelatīvās sakarības metodi. Aprēķina formula:![]() ; kur
; kur ![]() aprēķināmais (tieši nezināmais) absolūtais lielums;
aprēķināmais (tieši nezināmais) absolūtais lielums; ![]() aprēķināšanai izmantojamais zināmais lielums, kas korelatīvi ir saistīts ar lielumu
aprēķināšanai izmantojamais zināmais lielums, kas korelatīvi ir saistīts ar lielumu ![]() ;
; ![]() saistību koeficients, kas iegūts empīriskā (pieredzes) ceļā un kas
skaitliski izsaka x un y pārmaiņu caurmēra attiecību.
saistību koeficients, kas iegūts empīriskā (pieredzes) ceļā un kas
skaitliski izsaka x un y pārmaiņu caurmēra attiecību.
4.3. Relatīvie lielumi
Par relatīviem lielumiem statistikā sauc vispārinošus rādītājus, kas raksturo konkrētu sabiedrisku parādību kvantitatīvās attiecībās. Aprēķina formula: ![]() ; kur
; kur ![]() koeficients;
koeficients; ![]() salīdzināmais lielums;
salīdzināmais lielums; ![]() bāze. To lielumu, ar kuru izdara salīdzināšanu, sauc par salīdzinājuma bāzi, jeb bāzes lielumu. Relatīvo lielumu iegūšanai var salīdzināt gan vienāda, gan arī dažāda nosaukuma absolūtos lielumus.
bāze. To lielumu, ar kuru izdara salīdzināšanu, sauc par salīdzinājuma bāzi, jeb bāzes lielumu. Relatīvo lielumu iegūšanai var salīdzināt gan vienāda, gan arī dažāda nosaukuma absolūtos lielumus.
Relatīvie lielumi
![]()
![]()
| Attiecinot vienāda nosaukuma absolūtos lielumus, iegūst:
| Attiecinot dažāda nosaukuma absolūtos lielumus veidojas:
|
4.3.1.att. Relatīvo lielumu grupas
Salīdzinot vienāda nosaukuma absolūtos lielumus, iegūst nenosauktus relatīvos lielumus:
- koeficientus (0,95; 1,268). Tie rāda ,cik reižu viens lielums lielāks (mazāks) par bāzes lielumu, vai kādu daļu tas veido no bāzes lieluma, ko statistika pieņem par 100;
- lai koeficientu izteiktu procentos (%), tas jāpareizina ar 100. Procenti ir visvairāk izplatītā relatīvo lielumu izteiksmes forma;
- promiles (), iegūst koeficientu reizinot ar 1000.
Salīdzinot dažāda nosaukuma lielumus iegūst nosauktos relatīvos lielumus, kas izteikti noteiktās mērvienībās. Piemēram, iedzīvotāju blīvumu raksturo ar iedzīvotāju skaitu uz 1 km2.
4.4. Relatīvo lielumu veidi
Izšķir vairākus relatīvo lielumu veidus:
- dinamikas relatīvie lielumi raksturo sabiedrisko parādību attīstību laikā;
- struktūras relatīvie lielumi raksturo statistiskā kopuma sastāvu (uzbūvi), piemēram, uzņēmuma darbinieku sastāvs pēc to nodarbinātības;
- plāna uzdevuma relatīvie lielumi rāda, cik reižu vai par cik procentiem paredzētie rādītāji pārsniedz tos rādītājus, kuri faktiski sasniegti iepriekšējā periodā;
- plāna izpildes relatīvie lielumi raksturo plāna uzdevuma izpildes pakāpi;
- salīdzinājuma relatīvie lielumi raksturo vienas parādības lieluma salīdzinājuma rezultātus uz vienu un to pašu laika periodu, bet uz dažādiem objektiem vai teritorijām.
Piemēram, salīdzinot dažādu valstu ekonomiskos rādītājus.
Salīdzinājums ir viens no galvenajiem jebkuras analīzes paņēmieniem.
Salīdzinājuma relatīvos lielumus iegūst attiecinot divus absolūtos lielumus vai attiecinot divus relatīvos lielumus (augšanas tempus),tādā veidā iegūts rādītājus sauc par apsteidzes tempiem:
- koordinācijas relatīvais lielums raksturo vienota procesa koordinējoši pretēju izpausmi, piemēram, eksporta attiecība pret importu;
- intensitātes relatīvie lielumi raksturo vienas parādības izplatības pakāpi kādā citā ar to saistītā parādībā (vidē).
Kopējo un atšķirīgo aprēķinos attēlo sekojošā tabula:
4.4.1.tabula. Relatīvo lielumu klasificējošās īpatnības
| Relatīvo lielumu veids | Attiecības skaitītājam un saucējam | |
| Kopējs | Atšķirīgs | |
| Struktūras | objekts, pazīme, laiks | Apjoms: Kopuma daļa Viss kopums |
| Dinamikas | objekts, tā apjoms, pazīme | Laiks: Pārskata periodā Bāzes periodā |
| Salīdzinājumu | pazīme, laiks | Objekts: Viens objekts Otrs objekts |
| Koordinācijas | objekts, pazīme, laiks | Apjoms: Viena daļa Otra daļa |
| Plāna izpildes | objekts, pazīme | Pazīmes raksturs: Izpilde Plāns |
| Plāna uzdevuma | objekts, pazīme | Pazīmes raksturs, laiks Plāna uzdevums Izpilde bāzes periodā |
| Intensitātes t.sk .ekonomiskās attīstības | objekts, laiks | Pazīme: Viena pazīme Otra pazīme |
Statistikas praksē rēķina arī relatīvo lielumu starpības. Relatīvo lielumu starpība rāda , cik lielas ir salīdzināmo objektu (periodu) relatīvo raksturojumu absolūtās atšķirības.
Relatīvo lielumu starpības izsaka punktos:
- procentu punkti (%p);
- promiļu punkti (p).
Jāievēro, ka absolūtos un relatīvos lielumus statistiskā pielieto kompleksi, tādēļ svarīgi iegaumēt sekojošus absolūto un relatīvo rādītāju izmantošanas principus:
- stabila relatīvo lielumu bāze;
- salīdzināmo lielumu atbilstība;
- vienāda aprēķināšanas metodika;
- vienādas mērvienības;
- sezonalitāte;
- teritoriālās un organizatoriskās pakļautības salīdzināmība.
5. Centrālās tendences rādītāji
Sabiedrisko parādību raksturīga īpatnība ir to dažādība, atšķirība, variācija.
Piemēram, viena uzņēmuma darbinieki atšķiras pēc vecuma, darba stāža, izglītības u.tml. Tāpat preču cenas var būt atšķirīgas dažādos veikalos, dažādos laika periodos.
Taču, neskatoties uz to, konkrētos apstākļos, konkrētiem objektiem dotajā kopumā ir arī kaut kādas raksturīgas kopīgas pazīmes līmeņi. Pazīmes apjomu, kāds raksturīgs visai pētāmo vienību masai, statistiski raksturo ar vidējiem lielumiem, kas ir viens no centrālās tendences rādītājiem. Savukārt, centrālās tendences rādītāji ir viena no aprakstošās statistikas kategorijām.
Aprakstošā statistikas klasifikācija ir šāda.
Biežuma sadalījums:
- Procentuālās frekvence.
- Relatīvās frekvences
Centrālās tendences
rādītāji (vidējie lielumi):
- Vidējais aritmētiskais.
- Moda
- Mediāna
Dispersijas rādītāji (izkliedes rādītāji):
- Amplitūda (range).
- Dispersija (variance).
- Standartnovirze (standard deviation).
Normalitātes rādītāji (measures of normality):
- Asimetrijas koeficients, A (skewness).
- Ekscesa koeficients, E (kurtosis).
5.1. Vidējo lielumu veidi
Statistiskie vidējie lielumi ir vispārinoši rādītāji, kas izsaka masveida parādību tipiskos, raksturīgos līmeņus un stāvokļus konkrētos vietas un laika apstākļos.
Tātad vidējais lielums raksturo to centrālo tendenci, dod iespēju salīdzināt dažādus kopumus, objektus. Tos lieto arī dinamikas pētījumos un statistiski nosakot sakarības starp parādībām.
Vidējā lieluma īpašības:
- vidējais lielums vienmēr ir daudzu lielumu vidējais;
- vidējā
lielumā izpaužas lielā skaita likuma darbība - sedzas nejaušo faktoru
izsaukto skaitlisko vērtību novirzes un izpaužas būtisko faktoru
izsauktās tipiskās, raksturīgās vērtības;
- vidējos lielumus rēķina kvalitatīvi viendabīgam kopumam;
- vidējais lielums ir daudzu un dažādu individuālo viena un tā pašā veida lielumu vidējais lielums.
Pastāv divu veidu vidējie lielumi:
- pakāpju vidējie;
- struktūras vidējie.
Pakāpju vidējie rādītāji ir:
- aritmētiskais vidējais;
- ģeometriskais vidējais;
- kvadrātiskais vidējais;
- harmoniskais vidējais u.c.
Struktūras vidējie rādītāji ir:
- moda;
- mediāna;
- kvartile.
Vidējie lielumi
Pakāpju vidējie lielumi – visizplatītākais ir vienkāršais aritmētiskais vidējais, ko aprēķina pēc formulas: 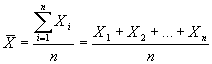 , kur
, kur ![]() aritmētiskais vidējais;
aritmētiskais vidējais; ![]() variante;
variante; ![]() kopas vienību skaits.
kopas vienību skaits.
Ģeometriskais vidējais – to galvenokārt lieto dinamikas analīzē, raksturo pētāmās parādības vidējo attīstības ātrumu (vidējo augšanas tempu). Aprēķina pēc formulas: ![]() , kur
, kur ![]() ģeometriskais vidējais;
ģeometriskais vidējais; ![]() dinamikas rindas līmeņu skaits;
dinamikas rindas līmeņu skaits; ![]() dinamikas rindas līmeņi (augšanas tempi).
dinamikas rindas līmeņi (augšanas tempi).
Vidējā ģeometriskā aprēķināšanas piemērs (nosacīti dati):
5.1.1.tabula. Uzņēmuma A eksports no 2012.gada līdz 2016.gadam, tūkst. EUR
| Gadi | 2012 | 2013 | 2014 | 2015 | 2016 |
| Eksports | 15 634 | 25 867 | 37 450 | 27 889 | 17 278 |
![]()
![]()
Secinājums. Eksports katru gadu vidēji palielinājies par 28%.
Kvadrātiskais vidējais – to izmanto tad, ja dati, kuru vidējais jāatrod, ir radušies, rēķinot novirzes no kāda cita vidējā. Šo vidējo lieto sadalījuma rindas pazīmes individuālo nozīmju variāciju pētīšanā. Aprēķina pēc formulas: 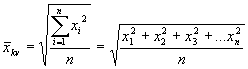 , kur
, kur ![]() kvadrātiskais vidējais;
kvadrātiskais vidējais; ![]() sadalījuma rindas līmeņu skaits;
sadalījuma rindas līmeņu skaits; ![]() pazīmes vērtība jeb novirze no
pazīmes vērtība jeb novirze no ![]() .
.
Harmonisko vidējo aprēķina pēc formulas: 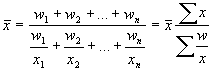 ,
, 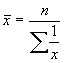 kur
kur ![]() vidējais;
vidējais; ![]() summas zīme;
summas zīme; ![]() varianti skaits;
varianti skaits; ![]() varianti;
varianti; ![]() varianta un biežuma reizinājums (kopējais).
varianta un biežuma reizinājums (kopējais).
Vienkāršos aritmētiskos vidējos lieto, aprēķinot vidējos lielumus nesagrupētiem datiem.
Sociālekonomiskajos aprēķinos harmoniskā vidējā lietošana nepieciešama tad, ja nav tiešas sākotnējās informācijas, kas būtu piemērota aritmētiskā vidējā aprēķināšanai.
5.1.1. Praktiskais darbs ar atbildi. Vidējā aritmētiskās aprēķināšana.
Ir atlasīti pieci uzņēmumi, n=5, kuros strādā šāds darbinieku skaits 46, 54, 42, 46, 32.
x1 = 46 x2 = 54 x3 = 42 x4 = 46 x5 = 32
Tātad summējot iegūstam kopējo darbinieku skaitu 220, ko izdalām ar 5. Tātad vidējais darbinieku skaits ir 44.
5.1.2. Praktiskais darbs ar atbildi. Vidējā aritmētiskās aprēķināšana.
Pieņemsim, ka doti 10 darbinieku ienākumi, EUR (noapaļoti līdz tuvākajam simtam).
5.1.2. tabula. Sākotnējie dati.
|
Pazīmes nr. |
Ienākumi, EUR |
Pazīmes nr. |
Ienākumi, EUR |
|
1. |
400 |
6. |
700 |
|
2. |
500 |
7. |
200 |
|
3. |
700 |
8. |
400 |
|
4. |
800 |
9. |
1000 |
|
5. |
1200 |
10. |
700 |
Lai aprēķinātu vidējo aritmētisko, summējam visu darbinieku ienākumus kopā. Iegūstam 6600 €, tad dalām ar kopējo pazīmju skaitu (n = 10), iegūstam vidējo aritmētisko 660 €.
Vidējā aritmētiskā īpašība ir, ka mainoties jebkuras pazīmes absolūtajai vērtībai, mainās arī vidējā aritmētiskās vērtība. Varam teikt, ka vidējais aritmētiskais ir ļoti "demokrātisks” rādītājs.
Gadījumos, kad variāciju rindā ir viena vai divas ekstrēmas vērtības vidējais aritmētiskais, kā variāciju rindas novērtējuma rādītājs mums nederēs.
Piemērs. Pieņemsim, ka pazīmei nr. 10 vērtība ir nevis 700, bet 7000 EUR.
5.1.3. tabula. Dati ar ekstrēmu vērtību
|
Pazīmes nr. |
Ienākumi, EUR |
Pazīmes nr. |
Ienākumi, EUR |
|
1. |
400 |
6. |
700 |
|
2. |
500 |
7. |
200 |
|
3. |
700 |
8. |
400 |
|
4. |
800 |
9. |
1000 |
|
5. |
1200 |
10. |
7000 |
Iegūstam, ka kopējie darbinieku ienākumi ir 12 900 €, bet vidējais aritmētiskais ir 1290 €. Deviņas no desmit pazīmēm ir mazākas par iegūto skaitli. Tas ir netipisks vidējais.
5.2. Svērtais aritmētiskais vidējais
Ja dati ir sagrupēti un pazīmes atsevišķās skaitliskās nozīmes atkārtojas vairāk reižu un pie tam nevienādā skaitā, vidējo aprēķina kā svērto aritmētisko vidējo. Ja variantes ir grupētas intervālos (no... līdz...), tad par varianšu skaitliskajām vērtībām nosacīti pieņem lielumus, kas atbilst intervālu vidum, kuru aprēķina kā aritmētisko vidējo starp intervāla zemāko un augstāko vērtību. Nenoslēgtos intervālus vispirms noslēdz, vadoties pēc analoģijas ar sekojošo vai iepriekšējo nenoslēgto intervālu.
Svērto aritmētisko vidējo aprēķina pēc formulas: 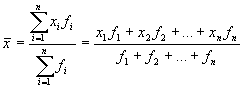 , kur
, kur ![]() aritmētiskais vidējais;
aritmētiskais vidējais; ![]() pazīmes nozīme vai intervāla vidējā nozīme;
pazīmes nozīme vai intervāla vidējā nozīme; ![]() variantes biežums jeb atkārtošanās reižu skaits.
variantes biežums jeb atkārtošanās reižu skaits.
Skaitļus, kas rāda, cik reižu (jeb cik bieži) sastopamas (atkārtojas) atsevišķas variantes, sauc par biežumiem jeb svariem. Varianšu reizināšanu ar to biežumiem statistikā sauc par "svēršanu", no tā arī cēlies svērtā aritmētiskā vidējā nosaukums. Aprēķinot svērto aritmētisko vidējo, absolūto lielumu vietā var lietot arī varianšu īpatsvarus, t.i. varianšu relatīvos biežumus.
Svaru izvēle.
Pēc varianšu un svaru atbilstības pakāpes iedalās - tiešie svari un nosacītie svari.
Tiešie svari - statistiskā kopuma vienības, kurām tieši un individuāli piemīt pētāmās pazīmes varianšu dažādie skaitliskie lielumi.
Nosacītie svari - lielumi, kas pēc satura arī ir cieši saistīti ar pētāmo pazīmi, taču to atbilstība variantēm izpaužas zināmā nosacījumā jeb pieņēmumā.
5.2.1. Pratiskais darbs ar atbildi.
Uzņēmuma Prudentia-Bache Securites akciju pārdošanas rezultāti biržā nedēļas laikā ir doti tabulā.
5.2.1. tabula. Aprēķināt pārdoto akciju svērto vidējo aritmētisko.
| Akcijas cena | Pārdoto akciju skaits |
|
| 16.00 | 12 | 192.00 |
| 21.00 | 16 | 336.00 |
| 18.00 | 8 | 144.00 |
| 13.00 | 15 | 195.00 |
| 12.00 | 9 | 108.00 |
| Kopā: | 60 | 975.00 |
Atbilde: 975.00 / 60 = 16.25 EUR
Ja pētāmajā kopā ietilpst liels novērošanas vienību skaits, sākotnējā informācija parādās sadalījuma rindas vai grupējumu veidā.
5.3. Moda un mediāna
Sabiedrisko parādību vispārinošai raksturošanai statistikā izmanto arī t.s. struktūras vidējos. Struktūras vidējie ir konkrētas variantes, kas pētāmās parādības tipisko līmeni izsaka ar kaut kādā ziņā zīmīgu stāvokli sadalījuma rindā.
Moda – variante, kurai sadalījuma rindā ir vislielākais biežums jeb svars.
Modu lieto tad, ja svarīgi izdalīt variantu, kurš sastopams visbiežāk. Modu neietekmē sadalījuma rindas ekstrēmās vērtības. Šo rādītāju izmanto, lai aprakstītu pētāmo parādību, jo rādītājam ir tieksme variēt, salīdzinot vienu izlasi ar otru.
Piemērs. Uzņēmējam svarīgi zināt, kāds ir vispieprasītākais apavu numurs. Ja zināms, ka visvairāk pērk 41 izmēra apavus, tas arī būs modālais lielums.
Diskrētā rindā moda nav jāaprēķina, bet jānolasa variante ar vislielāko biežumu.
Intervālu sadalījuma rindā modālā lieluma noteikšanai izmanto formulu: ![]() , kur
, kur ![]() moda;
moda; ![]() modālā intervāla zemākā robeža;
modālā intervāla zemākā robeža; ![]() modālā intervāla plašums (garums);
modālā intervāla plašums (garums); ![]() modālā intervāla biežums;
modālā intervāla biežums; ![]() pirmsmodālā intervāla biežums;
pirmsmodālā intervāla biežums; ![]() pēcmodālā intervāla biežums.
pēcmodālā intervāla biežums.
Intervālu rindā vispirms jānosaka modālais intervāls. Tas ir intervāls ar vislielāko biežumu sadalījuma rindā. Jo šaurāki intervāli, jo precīzāka moda. Moda būs modālā intervāla centrālais variants.
Mediāna – pazīmes skaitliskā vērtība, kāda tā ir ranžētas sadalījuma rindas vidū esošai vienībai. Pie tam sadalījuma rindu var ranžēt gan augoši, gan dilstoši. Tā attēlo vidējo vērtību, kur variāciju rinda
ir sadalīta divās līdzīgās daļās,
kur 50% no visām pazīmēm ir vienā pusē, bet otras 50% otrā pusē.
Diskrētā sadalījuma rindā mediānu, t.i. centrālo rādītāju, aprēķina, nosakot tās kārtas numuru: ![]() , kur
, kur ![]() gadījumu skaits.
gadījumu skaits.
Intervālu sadalījuma rindai mediānas noteikšanai izmanto formulu: 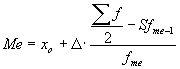 , kur
, kur ![]() mediāna;
mediāna; ![]() mediānas intervāla plašums (garums);
mediānas intervāla plašums (garums); ![]() mediānas intervāla zemākā robeža;
mediānas intervāla zemākā robeža; ![]() sadalījuma rindas locekļu summa;
sadalījuma rindas locekļu summa; ![]() pirmsmediānas intervāla uzkrātais biežums;
pirmsmediānas intervāla uzkrātais biežums; ![]() mediānas intervāla biežums.
mediānas intervāla biežums.
Mediānais intervāls – intervāls ranžētā sadalījuma rindā, kurā atrodas kopuma mediānā vienība.
Mediānu neietekmē sadalījuma rindas gan ekstrēmas, gan galējās vērtības, tāpēc mediānu lieto vērtējoša priekšstata iegūšanai gadījumos, ja pētāmās pazīmes vērtībām ir krasas atšķirības.
Mediānas aprēķināšana.
Attēlo vidējo vērtību, kur variāciju rinda ir sadalīta divās līdzīgās daļās. 50% no visām pazīmēm ir vienā daļas pusē, bet otras 50% otrā daļas pusē.
5.3.1. Pratiskais darbs ar atbildi. Mediānas aprēķināšana un modas aprēķināsana.
Lai iegūtu mediānu sarindojam pazīmju rindu pēc lieluma sākot no mazākās 200 €, līdz lielākai, 7000 €. Tālāk vienkārši sadalām iegūto variāciju rindu, kur vienā pusē ir 5 pazīmes, otrā pusē otras 5.
5.3.1. tabula. Ranžēta datu kopas rinda.
|
Pazīmes nr. |
Ienākumi, € |
Pazīmes nr. |
Ienākumi, € |
|
7. |
200 |
6. |
700 |
|
1. |
400 |
4. |
800 |
|
8. |
400 |
9. |
1000 |
|
2. |
500 |
5. |
1200 |
|
3. |
700 |
10. |
7000 |
No tabulas redzam, ka ranžētas sadalījuma rindas viduspunkts ir 700 € (pazīmes nr. 3. un 6.).
Šajā gadījumā mums abas vidējā punkta pazīmes ir vienādas 700 €. Gadījumā, ja viduspunkta vienas puses pazīme ir lielāka par otras puses pazīmi, mēs abas šīs pazīmes summējam un dalām ar 2.
Piemēram, ja pazīme nr. 3 ir 600 € (nevis kā tabulā 700 €), mediāna ir 650 €.
Tādejādi, mediāna mums atrisina jautājumu un dod precīzu variāciju rindas vidējā aprēķinu, gadījumā, ja mūsu variāciju rindā ir ekstrāmas vērtības.
Modas aprēķināšana.
Dotajā piemērā redzam, ka
atribūts "ienākumi" parādās visbiežāk divos gadījumos, kad tas ir 400 € (pazīmes 1. un 8.) un 700 € (pazīmes 3. un 6.), skat. 5.3.1. tabulu. No kā izriet, ka dotajā datu kopā ir 2 modas, - 400 €
un 700 €. Gadījumā, ja 1. pazīmes vērtība ir 300 €, tad datu kopā ir 1 moda, 700 €.
Tātad šis lielums mums reprezentē ienākuma modālo vērtību, vai teiksim, vistipiskāko vērtību.
5.4. Variācijas statistiskā analīze
Statistiskā kopuma raksturošanai nepietiek tikai ar vidējo lielumu, jo tajā izzūd pētāmās parādības atsevišķo vienību svārstības jeb variācijas.
Variācija – jebkuras statistiskās kopas īpašība- pazīmes skaitlisko un atributīvo nozīmju individuālā atšķirība, kuru izraisa dažādu faktoru ietekme. Mērīt variāciju nozīmē noteikt kopas vienību skaitlisko vērtību tuvības vai atšķirības pakāpi. Jo mazāka variācija, jo tipiskāks ir vidējais lielums un viendabīgāks kopums. Jo vairāk novirzās pazīmes individuālās vērtības no kopuma vidējā, jo netipiskāks ir vidējais lielums.
Variācijas mērīšanai statistikā izmanto vairākus variācijas rādītājus. Svarīgākie no tiem ir:
- variācijas apjoms jeb amplitūda;
- vidējā lineārā novirze;
- standartnovirze jeb vidējā kvadrātiskā novirze;
- dispersija;
- variācijas koeficients.
Variācijas apjoms ir starpība starp pazīmes lielāko un mazāko vērtību. ![]() , kur
, kur ![]() variācijas apjoms jeb amplitūda;
variācijas apjoms jeb amplitūda; ![]() pazīmes lielākā vērtība;
pazīmes lielākā vērtība; ![]() pazīmes mazākā vērtība. [1]
pazīmes mazākā vērtība. [1]
Vidējā lineārā novirze ![]() (alfa) ir aritmētiskais vidējais noatsevišķu varianšu absolūto noviržu no aritmētiskā vidējā.
(alfa) ir aritmētiskais vidējais noatsevišķu varianšu absolūto noviržu no aritmētiskā vidējā. 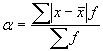 , kur
, kur ![]() vidējā lineārā novirze;
vidējā lineārā novirze; ![]() variantes biežums;
variantes biežums; ![]() kopas vienību skaits;
kopas vienību skaits; ![]() grupas vidējā vērtība;
grupas vidējā vērtība; ![]() pazīmes aritmētiskais vidējais. [2]
pazīmes aritmētiskais vidējais. [2]
Dispersija ![]() ir atsevišķu varianšu noviržu no aritmētiskā vidējā kvadrātu vidējais lielums.
ir atsevišķu varianšu noviržu no aritmētiskā vidējā kvadrātu vidējais lielums. 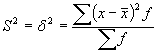 , kur
, kur ![]() dispersija;
dispersija; ![]() variantes biežums;
variantes biežums; ![]() kopas vienību skaits;
kopas vienību skaits; ![]() grupas vidējā vērtība (rindas gadījumā – intervāla vidējā nozīme);
grupas vidējā vērtība (rindas gadījumā – intervāla vidējā nozīme); ![]() pazīmes aritmētiskais vidējais.
pazīmes aritmētiskais vidējais.
Apzīmējumu ![]() lieto, ja dispersiju rēķina izlases datiem. [3]
lieto, ja dispersiju rēķina izlases datiem. [3]
Standartnovirze jeb vidējā kvadrātiskā novirze – ir visizplatītākais variācijas rādītājs. Tā ir kvadrātsakne no dispersijas un parāda, kā izvietojas vienību galvenā masa attiecībā pret vidējo. 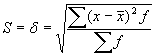 , kur
, kur ![]() dispersija;
dispersija; ![]() variantes biežums;
variantes biežums; ![]() kopas vienību skaits;
kopas vienību skaits; ![]() grupas vidējā vērtība;
grupas vidējā vērtība; ![]() pazīmes aritmētiskais vidējais. [4]
pazīmes aritmētiskais vidējais. [4]
Ja pētījumā izšķiroša nozīme ir relatīvās variācijas novērtēšanai, jālieto relatīvās variācijas rādītāji, variācijas koeficients, kurš izsaka variācijas salīdzinošu pakāpi. To izsaka procentos. Ja variācijas koeficients nepārsniedz 33 %, tad statistiskais kopums ir viendabīgs. Aprēķina formula:![]() , kur
, kur ![]() variācijas koeficients;
variācijas koeficients; ![]() grupas vidējā vērtība.
grupas vidējā vērtība.
5.4.1. Praktiskais darbs ar atbildi. Dispersijas un standartnovirzes aprēķins.
Dota izlases, n= 17 datu kopa:
| 32.2 |
29.5 |
29.9 |
32.4 |
30.5 |
30.1 |
32.1 |
35.2 |
10.0 |
20.6 |
28.6 |
30.5 |
38.0 |
33.0 |
29.4 |
37.1 |
28.6 |
|---|
Arēķināt vidējo aritmētisko, dispersiju un standartnovirzi.
Aprēķinot izmantojam [4] vienādojumu.
Vidējais aritmētiskais = 29.86
Dispersija, S2 = (32.2 - 29.86)2 + (29.5 - 29.86)2 + (29.9 - 29.86)2 + (29.9 - 29.86)2 + ....+ (28.6 - 29.86)2 / 17 -1 = 658.5592 / 16 = 41.15995
Standartnovirze, S = \( \sqrt[]{41.15995} \) = 6.42
6. Savstarpējo sakarību analīze
Statistikas uzdevums ir pētīt sabiedrisko parādību savstarpējās sakarības. Ar statistiskajām metodēm iespējams ne vien konstatēt šādas sakarības, bet arī skaitliski izteikt to raksturu un pakāpi.
Ja kādas vienas pazīmes pārmaiņa rada arī citas pazīmes pārmaiņu, tas nozīmē, ka šīs pazīmes ir savstarpēji saistītas jeb korelē.
Piemērs. Eksistē korelācija strap dzīves līmeņa pieaugumu un izdevumiem atpūtai un tūrismam.
6.1. Savstarpējo sakarību būtība, veidi un formas
Sabiedriskās parādības vai to pazīmes, kas ietekmē citas parādības un izraisa to pārmaiņas, sauc par faktoriālām parādībām, bet tās parādības (pazīmes), kas mainās faktoriālo parādību ietekmē, sauc par rezultatīvām parādībām (pazīmēm).
Atkarībā no pētāmo parādību sakarības ciešuma statistikā izšķir pilno jeb funkcionālā sakarību un korelatīvo sakarību [J.Vītols, 1998.].
Funkcionālās sakarības būtība ir tāda, ka katrai kādas faktoriālās pazīmes ![]() vērtībai atbilst pilnīgi noteikta rezultatīvās pazīmes
vērtībai atbilst pilnīgi noteikta rezultatīvās pazīmes ![]() vērtība. Funkcionālās sakarības pastāv precīzajās zinātnēs- matemātikā, fizikā.
vērtība. Funkcionālās sakarības pastāv precīzajās zinātnēs- matemātikā, fizikā.
Sakarības, kas novērojamas ekonomikā, veidojas daudzu apstākļu ietekmē, pie kam nav precīzi zināms, cik lielā mērā katrs no tiem ietekmē rezultātu .Šādas sakarības sauc par korelatīvām sakarībām.
Atkarībā no virziena izšķir tiešu un pretēju sakarību.
Ja pastāv tieša sakarība, tad palielinoties faktoriālās pazīmes vērtībai, palielinās arī rezultatīvās pazīmes vērtība. Parādību pretējas sakarības gadījumā, palielinoties faktoriālās pazīmes vērtībai, rezultatīvās pazīmes vērtība samazinās.
Pēc analītiskās izteiksmes veida izšķir lineāru jeb taisnvirziena sakarību un nelineāru sakarību.
Par lineāru sakarību sauc sakarību, kad vairāk vai mazāk vienmērīgai faktoriālās pazīmes pārmaiņai seko tāda pati rezultatīvās pazīmes pārmaiņa. Matemātiski šāda sakarība atbilst lineāram vienādojumam, un grafiski to var attēlot ar taisni.
Nelineāras sakarības gadījumā vienmērīgām faktoriālās pazīmes pārmaiņām seko nevienmērīga rezultatīvās pazīmes pārmaiņa. Pēc savas ģeometriskās formas šāda sakarība atgādina līkni (parabolu, hiperbolu vai citu).
Vienkāršākais korelatīvās sakarības veids ir pāra jeb vienkāršā korelācija- sakarība starp divām pazīmēm- rezultatīvo un faktoriālo.
Lai noskaidrotu divu vai vairāku faktoru ietekmi uz rezultātu, izmanto daudzfaktoru korelāciju.
Sakarības ciešuma novērtēšanai izmanto korelācijas koeficientu ![]() . Jo koeficients ir tuvāk 1, jo sakarība ciešāka, ja
. Jo koeficients ir tuvāk 1, jo sakarība ciešāka, ja ![]() , sakarība starp pētāmajām pazīmēm nepastāv.
, sakarība starp pētāmajām pazīmēm nepastāv.
Koeficients var mainīties robežās no ![]() līdz
līdz ![]() . Plusa zīme
. Plusa zīme ![]() norāda uz tiešu sakarību, mīnusa zīme
norāda uz tiešu sakarību, mīnusa zīme ![]() - sakarība ir pretēja.
- sakarība ir pretēja.
6.2. Savstarpējo sakarību atklāšanas metodes
Pētot savstarpējās sakarības, statistika risina divus uzdevumus:
1. nosaka sakarību esamību, konstatē to raksturu, izmantojot kādu no metodēm: grafisko metodi, paralēlo rindu metodi, analītisko grupēšanu vai veicot korelācijas un regresijas analīzi;
2. nosaka savstarpējo sakarību ciešumu un veic to skaitlisko raksturojumu, izmantojot korelācijas un regresijas analīzi.
Grafisko metodi izmanto, lai noteiktu sakarības raksturu un formu. Grafiskajā tīkliņā ar punktiem iezīmē pētāmā kopuma vienības. No punktu izvietojuma koordinātu sistēmā var spriest par sakarību starp pētāmajām pazīmēm.
Paralēlo rindu metodes būtība ir tāda, ka to izmantojot, salīdzina savā starpā divas vai vairākas variējošu rādītāju rindas, starp kurām loģiski iespējama sakarība.Ja pazīmes pārmaiņām atbilst rezultatīvās pazīmes pārmaiņas, tad var uzskatīt, ka starp šīm pazīmēm pastāv sakarība.
Analītiskās grupēšanas gadījumā kopuma vienības sadala grupās pēc faktoriālās pazīmes. Katrā grupā jāaprēķina rezultatīvās pazīmes vidējās vērtības un tās jāsalīdzina. Rezultātus attēlo grafiski, izdarot secinājumu par sakarībām.
Sakarības ciešuma noteikšanai izmanto korelācijas un regresijas metodi.
Par korelāciju un regresiju analīzi sauc metožu kopumu, ar kuru palīdzību pēta kvantitatīvās sakarības starp mainīgajiem lielumiem, ja tās ir korelatīvas.
Lai izvēlētos pareizo formulu korelatīvas sakarības ciešuma noteikšanai, vispirms jānoskaidro mainīgo lielumu attiecību veids starp mainīgajiem.
Apskatīsim sakarību starp diviem mainīgajiem.
Ja abi mainīgie ir izteikti kvantitatīvi, tad sakarību ciešuma novērtēšanai lieto Pirsona korelācijas koeficientu: 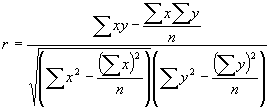
Statistikā lieto vēl citus koeficientus. Rezultāti būs atšķirīgi, kas izskaidrojams tādejādi, ka koeficientu aprēķināšanā lieto pazīmes vērtību dažādas izteiksmes.
Regresijas vienādojums ir matemātiskais modelis sakarībai starp korelatīvi saistītajiem mainīgajiem lielumiem.
Īsā laika posmā lielāko daļu sakarību var uztvert kā lineāras sakarības, tādēļ visbiežāk aprēķinu vienkāršošanai pētījuma sākumā izmanto lineāro funkciju: ![]() , kur
, kur ![]() neatkarīgais mainīgais lielums jeb faktoriālā pazīme;
neatkarīgais mainīgais lielums jeb faktoriālā pazīme; ![]() atkarīgais mainīgais lielums jeb rezultatīvā pazīme;
atkarīgais mainīgais lielums jeb rezultatīvā pazīme; ![]() regresijas brīvais loceklis, kas parāda aptuveno lielumu, kāds raksturīgs atkarīgajam lielumam bez faktoriālās pazīmes ietekmes;
regresijas brīvais loceklis, kas parāda aptuveno lielumu, kāds raksturīgs atkarīgajam lielumam bez faktoriālās pazīmes ietekmes; ![]() regresijas sakarības skaitliskā vērtība, kas norāda proporciju, kādā mainīsies rezultatīvā pazīme, mainoties faktoriālajai pazīmei par vienu vienību. Normālvienādojumu sistēmas atrisināšanai jāizskaitļo šādas formulas:
regresijas sakarības skaitliskā vērtība, kas norāda proporciju, kādā mainīsies rezultatīvā pazīme, mainoties faktoriālajai pazīmei par vienu vienību. Normālvienādojumu sistēmas atrisināšanai jāizskaitļo šādas formulas:
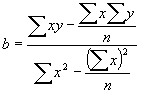 ;
; ![]() .
.
Aprēķinātais regresijas vienādojums būs piemērots konkrētam pētījumam, ja tā vidējā standartkļūda būs mazāka par rezultatīvās pazīmes vidējo kvadrātisko nozīmi.
Aprēķinot determinācijas koeficientu, t.i. kāpinot kvadrātā aprēķināto korelācijas koeficientu, un to izsakot procentos, var iegūt pētāmās pazīmes procentuālo daļu, kura atkarīga no faktoriālās pazīmes.
7. Izlase
Daudzi cilvēki intuitīvi saprot, ko nozīmē izlase, ko ģenerālā kopa. Pieņemsim, ka mums grozā ir 50 āboli. Lai secinātu, kāda ir ābolu garša, vai tie ir saldi, vai skābi, vai sulīgi (man personīgi garšo sulīgi āboli), mums nepieciešams izņemt dažus un nogaršot. Pieņemsim tiek izņemti pieci āboli no kuriem 3 ir sulīgi, bet 2 skābi. Ko varam secināt? Kādi āboli mums ir grozā? Pirmais tuvinājums, ka 3/5 ābolu ir sulīgi, bet 2/3 skābi. Ja mums būtu iespēja iekosties katrā ābolā un to nogaršot, mēs varētu pateikt precīzi, cik īsti ir sulīgie āboli, cik skābie. Nogaršojot 5 ābolus, mani secinājumi būs tikai varbūtīgi.
Statistiski novērojamie objekti parasti ir ļoti lieli, tos novērot pilnībā ir ļoti grūti un dārgi. Ir objekti, kuru pilnīga novērošana nav iespējama ne vien praktiski, bet arī teorētiski. Tādēļ statistika izmanto zinātniski pamatotus paņēmienus, ar kuru palīdzību, novērojot tikai daļu objekta vienību, var pietiekoši pamatoti spriest par visa pētāmā objekta raksturīgām īpašībām.Statistikā izlases metode ir viena no pētīšanas metodēm.
7.1. Ģenerālā kopa un izlases metode
Ģenerālā kopa jeb populācija (angl. – population) ir viendabīgu statistiskās izziņas objektu kopa, par kuru vēlas iegūt statistisko informāciju, un, kuras struktūru var pētīt ar izlases metodi. Ģenerālā kopa var būt galīga un eksistēt reāli.
Hipotētiskā kopa ir tāds statistisks objekts,
par kuru vēlas iegūt statistisku informāciju, bet kurš, atšķirībā no
galīgās ģenerālās kopas, nav ierobežots.
Izlases metode jeb izlase (angl. – sample, sample frame) ir pētīšanas metode, ar ko, novērojot daļu no ģenerālās kopas, iespējams iegūt reprezentatīvus pētāmā objekta raksturojošos rādītājus.
Ja ģenerālā kopā ir relatīvi neliela, pētnieks izvēlas visu kopu, - pilnīga statistiskā novērošana. Ja liela, tad izvēlas nejaušu izlasi (angl. – random sample), - nepilnā statistiskā novērošana, kur ikvienam ģenerālās kopas elementam ir iespēja tikt izvēlētam un analizētam. Rezultāti tiek vispārināti un atteicināti uz ģenerālo kopu. Izlase veidošanas matemātiskais pamats ir varbūtību teorija.
Nepilnās statistiskās novērošanas rezultātā ievāc datus nevis par
visām, bet tikai par daļu no ģenerālā vai hipotētiskā kopuma vienībām.
Izlases novērošana ir nepilnās novērošanas veids.
Izlases novērošanas mērķis ir iegūt objektīvu, zinātniski pamatotu informāciju par visu ģenerālo kopumu (statistiskā pētījuma objektu), no kura ņemta izlase.
Tātad par izlasi jeb izlases kopu sauc to ģenerālā kopuma daļu, kuru praktiski novēro, jeb tā ir pētīšanas metode, ar kuru, novērojot daļu no pētāmā objekta vienībām, iespējams iegūt reprezentatīvus pētāmo objektu raksturojošus rādītājus, kas ļauj spriest par visa ģenerālā kopuma īpašībām. Ar izlases metodes palīdzību:
- Izveido izlasi.
- Organizē plašu izlases novērošanas procesu.
- Aprēķina izlases reprezentācijas kļūdas.
Lai veidotu izlasi, jārisina virkne metodoloģijas jautājumu:
- Ģenerālās kopas robežas noteikšana.
- Izlases novērošanas programmu un instrukciju izstrādāšana.
- Izlases bāzes noteikšana.
- Kļūdas pieļaujamā lieluma aprēķināšana.
- Izlases apjoma aprēķināšana.
- Izlases novērošanas veida un laika noteikšana.
- Izlases novērošanas veikšanai nepieciešamo resursu noteikšana.
- Izlases datu precizitātes un ticamības novērtēšana.
Parasti tiek izmantoti šādi apzēmējumi:
N – ģenerālās kopas elementu skaits.
n – izlases elementu skaits.
Rādītājus, kurus aprēķina pēc izlases datiem, sauc par izlases raksturotājiem, arī vērtējumiem. Izlasi un ģenerālo kopumu var raksturot ar šiem statiskajiem rādītājiem (izlases raksturotājiem):- aritmētisko vidējo;
- modu;
- mediānu;
- dispersiju;
- standartnovirzi utt.
Rādītājus, kuri aprēķināti pēc ģenerālā kopuma datiem, sauc par kopuma parametriem.
Izlases metodes priekšrocības:
- ātrāk iespējams iegūt informāciju par kopām, kuras pilnībā novērot nav iespējams;
- ātrāk var veikt novērošanu;
- samazinās ar statistikas darbu saistītie izdevumi;
- sakarā ar mazāku darbu, iespējams rūpīgāk vadīt un kontrolēt novērošanu;
- iegūst augstu rezultātu ticamību;
- var paplašināt novērošanas programmu.
Viens no būtiskākajiem datu analīzes mērķiem ir, izmantojot izlase vidējo vērtību un izlase īpatsvaru noteikt attiecīgo gadījumlielumu visai ģenerālai kopai jeb ģenerālās kopas parametru.
Ja no katras ģenerālās kopas ņem pietiekami daudz vienas un tā paša lieluma izlases un katrai izlasei aprēķina aritmētisko vidējo, tad šādi aprēķinātie aritmētiskie vidējie ir gadījumlielums.
7.2. Izlašu veidi
Izlases veids ir atkarīgs no pētāmās pazīmes vienību atlases paņēmiena un kārtības no ģenerālā kopuma.
- Pēc atlases tehnikas izšķir īsti nejaušo jeb loterijas veida atlasi un mehānisko atlasi.
- Pēc novērojamo vienību atlases atkārtošanās klasificējas atkārtota izlase un neatkārtota izlase.
- Pēc pētāmo vienību atlases, atlase var būt individuālā un grupveida.
- Atkarībā no atlases (uzreiz vai pakāpeniski) vienpakāpju izlase un daudzpakāpju izlase.
Praksē, ņemot vērā dažādas īpatnības, visbiežāk lieto sekojošus izlašu veidus:
- īsti nejaušā vai vienkāršā gadījumizlase;
- mehāniskā izlase;
- tipoloģiskā jeb stratificētā izlase;
- sērijveida jeb ligzdveida izlase;
- daudzfāzu izlase;
- daudzpakāpju izlase;
- kombinētā izlase.
Īsti nejaušā izlase vislabāk nodrošina visu kopuma vienību vienādu iespēju nokļūt izlasē. Teorētiski vispamatotākais izlases veids. Atlase var būt gan atkārtota, gan neatkārtota. Palielinot novērojamo vienību skaitu, kļūdas samazinās. Ja izlases kopas vienību skaits ![]() , tad izlasi uzskata par mazu. Liela apjoma izlasē
, tad izlasi uzskata par mazu. Liela apjoma izlasē ![]() .
.
| ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■■ ■ |
7.2.1.att. Nejaušās izlases grafiskais attēlojums.
Mehānisko izlasi parasti lieto tad, ja atlase jāizdara no neierobežota (hipotētiska) ģenerālā kopuma. Visas vienības tiek sakārtotas pēc kādas būtiskas pazīmes augošā vai dilstošā kārtībā, atlase notiek ik pēc noteikta intervāla.
| ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ |
7.2.2.att. Mehāniskās izlases grafiskais attēlojums.
Tipoloģiskās izlases veidošanā , visu ģenerālo kopumu vispirms sadala tipiskās, iekšēji pēc iespējas vienveidīgās grupās. Vienību atlasi veic katras grupas ietvaros atsevišķi. Tipoloģiskā izlase ir viens no izplatītākajiem izlases veidiem. Tās paveidi: proporcionālā izlase; vienmērīgā izlase; vidējai kvadrātiskai novirzei proporcionālā izlase.
|
■ ■ ■ ■
■ ■
■ ■ |
■ ■ ■ ■ |
|
■ ■ ■
■ |
7.2.3.att. Tipoloģiskās izlases grafiskais attēlojums.
Sērijveida izlasi visbiežāk lieto tad, ja ģenerālais kopums dabiski dalās novērojamo vienību apakškopās, kuras nav iespējams dalīt.
|
|
7.2.4.att. Sērijveida izlases grafiskais attēlojums.
Daudzpakāpju izlase veidojas, izlases kopumu veidojot pakāpeniski. Pirmajā pakāpē atlasa sērijas, otrajā pakāpē- mazāka apjoma sērijas. Pēdējā pakāpē-novērojamās kopuma vienības. Jo vairāk pakāpju izlasei, jo lielāka kopējā kļūda un jo grūtāk to aprēķināt.
|
|
7.2.5.att. Daudzpakāpju izlases grafiskais attēlojums.
Daudzfāzu izlase izmanto principu - jo plašāka un sarežģītāka ir novērošanas programma, jo mazākam ir jābūt novērošanas vienību skaitam izlasē un otrādi.
Katrā fāzē izmanto vienu un to pašu izlases vienību. Novērojamo vienību skaits ir diferencēti saistīts ar novērošanas programmas plašumu un sarežģītību.
Kombinētā izlase - vairāku atlases paņēmienu kombinēšana. Izlases metodes trūkums, salīdzinot ar pilno novērošanu, ir izlases jeb reprezentācijas kļūda.
Par reprezentācijas kļūdu sauc zināmu izlases un ģenerālā kopuma raksturotāju neatbilstību, kas rodas sakarā ar to, ka šie kopumi nav vienādi. Tā ir starpība starp ģenerālās kopas parametru lielumu un lielumu, kas aprēķināts izlases novērošanas rezultātā. Reprezentācijas kļūdas lielums atkarīgs no:
- pazīmes nozīmes variācijas ģenerālajā kopā - jo lielāka pazīmes variācija, jo lielāka izlases kļūda un otrādi;
- izlases veida;
Izlases apjoma - jo lielāka izlase, jo mazāka izlases kļūda un otrādi.
Izlases kļūdu var izteikt absolūtās mērvienībās, relatīvās mērvienībās. Par absolūtās kļūdas rādītājiem izmanto standartkļūdu - 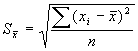 un robežkļūdu
un robežkļūdu ![]() , kur
, kur ![]() standartkļūda;
standartkļūda; ![]() jebkurš pētāmais kopas lielums;
jebkurš pētāmais kopas lielums; ![]() pētāmās kopas vidējais lielums;
pētāmās kopas vidējais lielums; ![]() pētāmās kopas vienību skaits;
pētāmās kopas vienību skaits; ![]() varbūtības koeficients.
varbūtības koeficients.
7.2.1. tabula. Biežāk lietojamās precizitātes varbūtības un to koeficienti.
| Varbūtība, % | 68 | 90 | 95 | 99 |
| Varbūtības koeficients | 1 | 1.64 | 1.96 | 2.58 |
Relatīvās kļūdas izsaka, kā absolūtās kļūdas attiecību pret kopas aritmētisko vidējo.
Reprezentācijas kļūdas var būt sistemātiskas un nejaušas.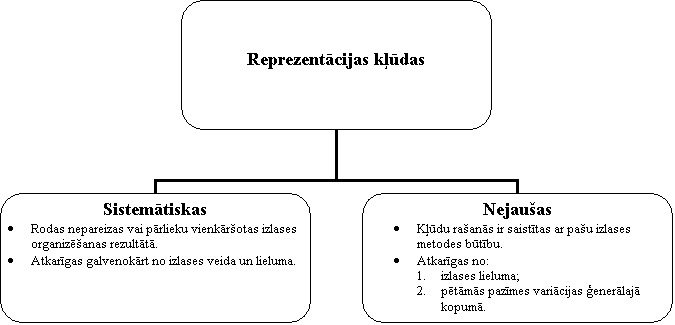
7.2.1. att. Reprezentācijas kļūdas veidi.
8. Dinamikas statistiskā izpēte
Svarīgs statistikas uzdevums ir pētīt ekonomisko parādību izmaiņas laikā, veidojot un analizējot dinamikas rindas.
Par dinamikas jeb laika rindām sauc statistisko datu rindas, kas raksturo statistikas objekta vai parādības izmaiņas laikā.
Dinamikas rindu veido divi elementi - laika norāde ![]() un parādības rindas līmenis
un parādības rindas līmenis ![]() . Atkarībā no tā, kādos lielumos izteikti dinamikas rindu līmeņi, izšķir absolūto lielumu; relatīvo lielumu; vidējo lielumu dinamikas rindas.
. Atkarībā no tā, kādos lielumos izteikti dinamikas rindu līmeņi, izšķir absolūto lielumu; relatīvo lielumu; vidējo lielumu dinamikas rindas.
Atkarībā no laika norādes izšķir momentu un intervālu dinamikas rindas.
Vidējo lielumu intervālu dinamikas rindas piemērs:
8.1.1. tabula. Strādājošo mēneša vidējā darba samaksa bruto, (y) pa visiem sektoriem pa mēnešiem, (t) no 2015M04 līdz 2016M03. gadā, EUR
|
t |
y |
|
2015M04 |
815 |
|
2015M05 |
802 |
|
2015M06 |
817 |
|
2015M07 |
863 |
|
2015M08 |
814 |
|
2015M09 |
810 |
|
2015M10 |
817 |
|
2015M11 |
816 |
|
2015M12 |
900 |
|
2016M01 |
814 |
|
2016M02 |
813 |
|
2016M03 |
854 |
Avots: LR Centrālās statistikas pārvalde [www.csb.gov.lv].
Momentu dinamikas rindas līmeņi izsaka parādības stāvokli noteiktā laika momentā, uz noteiktu datumu.
8.1. Dinamikas rindu līmeņu raksturojošie rādītāji
Dinamikas rindas līmeņu pārmaiņu raksturošanai izmanto virkni statistisko rādītāju. Svarīgākie diferencētie dinamikas rindas rādītāji ir:
- absolūtais pieaugums;
- augšanas temps;
- pieauguma temps;
- pieauguma 1 % absolūtā nozīme.
Diferencētos dinamikas rindas rādītājus pēc to aprēķināšanas rakstura iedala ķēdes un bāzes rādītājos.
Ķēdes rādītājus aprēķina secīgi salīdzinot (atņemot vai dalot) divus blakusesošos rindas līmeņus – sekojošo ar iepriekšējo
Bāzes rādītājus aprēķina secīgi salīdzinot katru nākošo rindas līmeni ar vienu par bāzi pieņemtu līmeni - tas parasti ir dotās rindas sākuma līmenis.
|
|
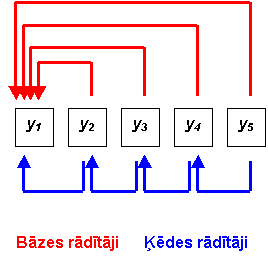

8.1.1.att. Ķēdes un bāzes rādītāju aprēķināšanas shēma
Absolūtais pieaugums ![]() izsaka dinamikas rindas līmeņa absolūto pārmaiņu palielināšanos vai samazināšanos salīdzinājumā ar kādu sasniegtu līmeni noteiktā laika periodā.
izsaka dinamikas rindas līmeņa absolūto pārmaiņu palielināšanos vai samazināšanos salīdzinājumā ar kādu sasniegtu līmeni noteiktā laika periodā.
Izšķir ķēdes un bāzes absolūto pieaugumu:
Ķēdes absolūtais pieaugums: ![]() , aprēķina no dinamikas kāda līmeņa atņemot šīs rindas iepriekšējo līmeni.
, aprēķina no dinamikas kāda līmeņa atņemot šīs rindas iepriekšējo līmeni.
Bāzes absolūtais pieaugums: ![]() ; aprēķina, no dinamikas rindas kāda līmeņa atņemot rindas sākuma līmeni, ko uzskata par bāzi, kur
; aprēķina, no dinamikas rindas kāda līmeņa atņemot rindas sākuma līmeni, ko uzskata par bāzi, kur ![]() apzīmē rindas pirmo (sākuma) līmeni;
apzīmē rindas pirmo (sākuma) līmeni; ![]() jebkuru dinamikas rindas līmeni.
jebkuru dinamikas rindas līmeni.
Augšanas koeficients, temps ![]() ir dinamikas rindas līmeņu relatīvo pārmaiņu rādītājs, raksturo pētāmās parādības attīstības ātrumu. Augšanas tempu izsaka koeficientu veidā vai %, pareizinot formulās norādīto līmeņu attiecību ar 100. Rāda, cik reizes attiecīgais rindas līmenis ir lielāks par bāzes līmeni (ja koeficients ir lielāks par vienu), vai kādu bāzes līmeņa daļu veido pārskata perioda līmenis (ja tas ir mazāks par vienu).
ir dinamikas rindas līmeņu relatīvo pārmaiņu rādītājs, raksturo pētāmās parādības attīstības ātrumu. Augšanas tempu izsaka koeficientu veidā vai %, pareizinot formulās norādīto līmeņu attiecību ar 100. Rāda, cik reizes attiecīgais rindas līmenis ir lielāks par bāzes līmeni (ja koeficients ir lielāks par vienu), vai kādu bāzes līmeņa daļu veido pārskata perioda līmenis (ja tas ir mazāks par vienu). ![]()
![]()
![]()
![]()
Augšanas koeficients un augšanas temps ir līmeņu pārmaiņu intensitātes divas formas, starpība starp tiem ir tikai mērvienībās.
Ķēdes augšanas temps: ![]() , aprēķina, dalot kādu dinamikas rindas līmeni ar šīs rindas iepriekšējo līmeni;
, aprēķina, dalot kādu dinamikas rindas līmeni ar šīs rindas iepriekšējo līmeni;
Bāzes augšanas temps: ![]() , aprēķina, dalot kādu dinamikas rindas līmeni ar rindas sākuma līmeni, ko uzskata par bāzi.
, aprēķina, dalot kādu dinamikas rindas līmeni ar rindas sākuma līmeni, ko uzskata par bāzi.
Pieauguma koeficients, temps ![]() ir augšanas tempa papildinājums un izsaka, par kādu veselā daļu vai par cik % mainījies attiecīgais rindas līmenis salīdzinājumā ar kādu citu jau sasniegtu līmeni. Pieauguma tempi var būt arī negatīvi skaitļi, un tādā gadījumā tie izsaka lielumu, par cik % pētāmā parādība samazinājusies.
ir augšanas tempa papildinājums un izsaka, par kādu veselā daļu vai par cik % mainījies attiecīgais rindas līmenis salīdzinājumā ar kādu citu jau sasniegtu līmeni. Pieauguma tempi var būt arī negatīvi skaitļi, un tādā gadījumā tie izsaka lielumu, par cik % pētāmā parādība samazinājusies.
Pieauguma tempu aprēķina pēc formulām – koeficienta: ![]() ;
; ![]() vai procentiem (%):
vai procentiem (%):![]() ;
;![]() .
.
Ja lieto augšanas koeficientu, aprēķina pēc formulas: ![]() un
un ![]()
Ja augšanas temps ir izteikts procentos (%), aprēķina pēc formulas: ![]() un
un ![]()
Pieauguma 1 % absolūtā nozīme izsaka pieauguma tempa reālo saturu, rāda, cik svarīgs ir katrs pieauguma procents ![]() . Saista absolūto pieaugumu un pieauguma tempu, aprēķina izmantojot formulu:
. Saista absolūto pieaugumu un pieauguma tempu, aprēķina izmantojot formulu: ![]() .
.
8.2. Dinamikas rindu vidējie rādītāji
Dinamikas rindu analīzē lieto arī vidējos rādītājus. Dinamikas rindas vidējais līmenis izsaka pētāmās parādības raksturīgo lielumu zināmā laika periodā. Dinamikas rindas vidējo līmeni sauc par hronoloģisko vidējo.
Dinamikas rindu vidējie lielumi raksturo dinamikas rindas īpašības visā aplūkojamā periodā. Lai aprēķinātu dinamikas rindas vidējos lielumus, jāpanāk vispārināmo vienību kopuma viendabīgums un pietiekams skaits.
Intervāla dinamikas rindai vidējo līmeni aprēķina kā vienkāršo aritmētisko vidējo: ![]() ; kur
; kur ![]() dinamikas rindas vidējais līmenis;
dinamikas rindas vidējais līmenis; ![]() dinamikas rindas līmeņi;
dinamikas rindas līmeņi; ![]() dinamikas rindu locekļu (līmeņu) skaits.
dinamikas rindu locekļu (līmeņu) skaits.
Intervāla dinamikas rindas ar vienāda ilguma laika periodiem – vidējo līmeni aprēķina pēc nesvērtā aritmētiskā vidējā: 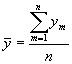 ; kur
; kur ![]() dinamikas rindas vidējais līmenis;
dinamikas rindas vidējais līmenis; ![]() jebkurš dinamikas rindas līmenis;
jebkurš dinamikas rindas līmenis; ![]() rindas līmeņu (momentu) skaits;
rindas līmeņu (momentu) skaits; ![]() pirmais dinamikas rindas līmenis.
pirmais dinamikas rindas līmenis.
Intervāla dinamikas rindas ar dažāda ilguma laika periodiem – vidējo līmeni aprēķina pēc svērtā aritmētiskā vidējā: 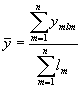 ; kur
; kur ![]() jebkurš dinamikas rindas līmenis;
jebkurš dinamikas rindas līmenis; ![]() rindas līmeņu skaits;
rindas līmeņu skaits; ![]() laika periods, kurā līmenis
laika periods, kurā līmenis ![]() ir nemainīgs;
ir nemainīgs; ![]() pirmais dinamikas rindas līmenis.
pirmais dinamikas rindas līmenis.
Momenta dinamikas rindas ar vienāda ilguma laika periodiem vidējo līmeni aprēķina pēc hronoloģiskā vidējā: 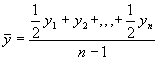 , kur
, kur ![]() līmeņu (momentu) skaits.
līmeņu (momentu) skaits.
Momenta dinamikas rindas ar dažāda ilguma laika periodiem – vidējo līmeni aprēķina pēc svērtā hronoloģiskā vidējā: 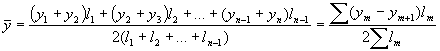 ; kur
; kur ![]() dinamikas rindas līmeņi;
dinamikas rindas līmeņi; ![]() laika periods, kurā līmenis ir nemainīgs.
laika periods, kurā līmenis ir nemainīgs.
Dinamikas rindas vidējo līmeni var arī aprēķināt kā vidējo no vidējiem lielumiem: 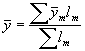
Vidējais absolūtais pieaugums ![]() ir pētāmās parādības pārmaiņas ātruma apkopojošs rādītājs laika vienībā. Tas izsaka, par kādu absolūtu lielumu vidēji laika vienībā pieaugusi vai samazinājusies pētāmā parādība visā ar dinamikas rindu aptvertajā periodā. Vidējo absolūto pieaugumu aprēķina kā nesvērto aritmētisko vidējo lielumu:
ir pētāmās parādības pārmaiņas ātruma apkopojošs rādītājs laika vienībā. Tas izsaka, par kādu absolūtu lielumu vidēji laika vienībā pieaugusi vai samazinājusies pētāmā parādība visā ar dinamikas rindu aptvertajā periodā. Vidējo absolūto pieaugumu aprēķina kā nesvērto aritmētisko vidējo lielumu: 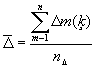 ; kur
; kur ![]() absolūto pieaugumu skaits;
absolūto pieaugumu skaits; ![]() ķēdes absolūto pieaugumu summa.
ķēdes absolūto pieaugumu summa.
Ja zināmi dati par pirmo un pēdējo līmeni, tad vidējo absolūto pieaugumu aprēķina: ![]() , kur
, kur ![]() absolūto pieaugumu skaits.
absolūto pieaugumu skaits.
Vidējais augšanas temps ![]() dinamikas rindas līmeņu izmaiņu intensitātes raksturotājs, tas raksturo pētāmās parādības attīstības vidējo intensitāti, rādot, cik reizes vidēji laika vienībā izmainījušies dinamikas rindas līmeņi. Vidējo augšanas tempu var aprēķināt pēc ģeometriskā vidējā formulas:
dinamikas rindas līmeņu izmaiņu intensitātes raksturotājs, tas raksturo pētāmās parādības attīstības vidējo intensitāti, rādot, cik reizes vidēji laika vienībā izmainījušies dinamikas rindas līmeņi. Vidējo augšanas tempu var aprēķināt pēc ģeometriskā vidējā formulas: ![]() ; kur
; kur ![]() ķēdes augšanas tempu skaits.
ķēdes augšanas tempu skaits.
Vidējā pieauguma temps ![]() rāda, par cik % vidēji palielinājies vai samazinājies pētāmās parādības līmenis visā pētāmajā periodā:
rāda, par cik % vidēji palielinājies vai samazinājies pētāmās parādības līmenis visā pētāmajā periodā: ![]() .
.
8.3. Dinamikas rindas izmaiņu tendences metodes
Svarīgs sociālekonomisko procesu likumsakarību pētīšanas virziens ir dinamikas rindas kopējās attīstības tendences – trenda noteikšana. Pētāmo objektu dinamikas rindu līmeņi svārstās – gan palielinās, gan samazinās. Šādos gadījumos, lai noteiktu trendu, lieto īpašas dinamikas rindu izlīdzināšanas metodes.
Trenda izzināšana nepieciešama lai pilnīgāk noskaidrotu pētāmās parādības attīstības raksturu, kāds faktiski bijis jau aizritējušā periodā, kā arī lai iegūtu teorētiski pamatotu bāzi dinamikas rindas turpināšanai, t.i., parādības prognozēšanai.
Trenda noteikšanai lieto speciālas metodes. Visplašāk lieto intervālu paplašināšanas, slīdošo vidējo un analītiskās izlīdzināšanas metodi.
Intervālu paplašināšanas metode saistīta ar sākotnējās dinamikas rindas pārveidošanu ilgstošāku periodu rindās (piemēram, dienas – mēneša, mēneša – ceturkšņa, ceturkšņa – gada u.t.t.). Šī metode ir pārāk elementāra. To var lietot tad, ja rinda, kuru pārveido, ir pietiekami gara.
Slīdošo vidējo metode. Arī šīs metodes pamatā ir intervālu paplašināšanas princips. Veidojot katru jaunu paplašinātu intervālu, tā sākuma punkts "paslīd" par vienu laika vienību uz priekšu. Šī metode piemērota tajos gadījumos, kad parādības attīstībai ir nevienmērīgs raksturs. Tā ļauj atbrīvoties no sezonālās ietekmes.
Analītiskā izlīdzināšanas metode ir visefektīvākā trenda atklāšanas metode. Tā ne tikai atklāj trendu, bet arī palīdz analizēt dinamikas rindu savstarpējo sakarību (korelāciju).
Dinamikas rindas analītiskā izlīdzināšana nozīmē, ka faktiskie dinamikas rindas līmeņi ![]() tiek aizvietoti ar teorētiskiem līmeņi
tiek aizvietoti ar teorētiskiem līmeņi ![]() . Ja faktiskos dinamikas rindas līmeņus attēlo grafiski, iegūst lauztu līniju, kas atspoguļo gan galveno tendenci, gan arī dažādas novirzes, kas radušās vai nu sezonas svārstību, vai citu faktoru rezultātā. Lai noskaidrotu galveno – pamattendenci, iztaisnošanu var veikt gan pēc taisnes, gan pēc kādas citas līnijas, kas atspoguļo dinamikas rindas līmeņu funkcionālo atkarību no laika. Atsevišķas funkcijas izvēles pamatā ir parādības būtības teorētiskā analīze un attīstības parādību likumi. Atkarībā no parādības attīstības tipa lieto noteiktu matemātiskās funkcijas veidu. Visbiežāk analītiskā izlīdzināšana notiek atbilstoši taisnes vienādojumam.
. Ja faktiskos dinamikas rindas līmeņus attēlo grafiski, iegūst lauztu līniju, kas atspoguļo gan galveno tendenci, gan arī dažādas novirzes, kas radušās vai nu sezonas svārstību, vai citu faktoru rezultātā. Lai noskaidrotu galveno – pamattendenci, iztaisnošanu var veikt gan pēc taisnes, gan pēc kādas citas līnijas, kas atspoguļo dinamikas rindas līmeņu funkcionālo atkarību no laika. Atsevišķas funkcijas izvēles pamatā ir parādības būtības teorētiskā analīze un attīstības parādību likumi. Atkarībā no parādības attīstības tipa lieto noteiktu matemātiskās funkcijas veidu. Visbiežāk analītiskā izlīdzināšana notiek atbilstoši taisnes vienādojumam.
Ja pētāmai parādībai ir vienmērīgs attīstības raksturs: ![]() ; kur
; kur ![]() izlīdzinātās rindas līmeņi, kurus vajag aprēķināt;
izlīdzinātās rindas līmeņi, kurus vajag aprēķināt; ![]() taisnes parametri;
taisnes parametri; ![]() laika rādītāji (dienas, mēneši u.t.t.).
laika rādītāji (dienas, mēneši u.t.t.).
Ja parādībai ir pakāpeniski paātrināts, augošs raksturs, izlīdzināšanu var izdarīt atbilstoši parabolas vienādojumiem.
Lai aprēķinātu izlīdzināšanai izraudzītās analītiskā vienādojuma konstantes ![]() un
un ![]() , jāsastāda un jāatrisina normālvienādojuma sistēmā:
, jāsastāda un jāatrisina normālvienādojuma sistēmā: 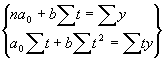 ; kur
; kur ![]() rindas locekļu skaits;
rindas locekļu skaits; ![]() laika periodi;
laika periodi; ![]() dinamikas rindas sākotnējie līmeņi.
dinamikas rindas sākotnējie līmeņi.
8.4. Sezonālo svārstību pētīšana
Dinamikas rindu analīzē svarīga nozīme ir sezonālām svārstībām . Sezonālās izmaiņas vērojamas gada ietvaros- pa mēnešiem, ceturkšņiem. Sezonālo svārstību analīzē izmanto indeksu metodi.
Sezonalitātes indeksu metode ![]() ; kur
; kur ![]() katras laika vienības līmenis;
katras laika vienības līmenis; ![]() pētāmo laika vienību vidējais līmenis.
pētāmo laika vienību vidējais līmenis.
Sezonalitātes dziļums 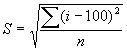 ; kur
; kur ![]() sezonalitātes indekss;
sezonalitātes indekss; ![]() laika vienību skaits.
laika vienību skaits.
Sezonalitātes pārmaiņu koeficients ![]() ; kur
; kur ![]() pētāmā gada sezonalitātes dziļums;
pētāmā gada sezonalitātes dziļums; ![]() iepriekšējā gada sezonalitātes dziļums. Ja
iepriekšējā gada sezonalitātes dziļums. Ja ![]() sezonalitāte padziļinājusies; ja
sezonalitāte padziļinājusies; ja ![]() sezonalitāte kļuvusi seklāka.
sezonalitāte kļuvusi seklāka.
9. Indeksi
Ekonomiskajā analīzē dažāda veida nesummējamu parādību analīzē nepietiek ar absolūto vai vidējo rādītāju salīdzināšanu. Jāizmanto īpaši indeksu metodes paņēmieni.
Indeksi ir relatīvi rādītāji, ar kuru palīdzību var noteikt dažāda veida nesummējamu parādību izmaiņas.
Piemēram, kā izmainījies dažādu veidu produktu kopējais apjoms, kā kopumā mainījušās cenas dažādu veidu precēm utt.
Analīzei nepieciešami rādītāji par diviem periodiem: bāzes un pārskata periodu. Formulās tos apzīmē attiecīgi ar zīmi "0"un "1".
Atšķirībā no citiem statistikas rādītājiem, indeksi:
- ļauj izmērīt saliktu sabiedrisku parādību izmaiņas;
- ļauj analizēt atsevišķu faktoru lomu parādības izmaiņā;
- ir salīdzinājuma rezultāti ne tikai ar iepriekšējo periodu, bet arī ar citu teritoriju, plānu, normatīviem.
9.1. Individuālie indeksi un kopindeksi
Statistikā izšķir individuālos indeksus un kopindeksus.
Individuālie indeksi (apzīmē ar mazo ![]() raksturo tikai vienas kopas elementa (vienkāršas parādības).
raksturo tikai vienas kopas elementa (vienkāršas parādības).
Piemēram, atsevišķu produkcijas veidu ražošanas vai realizācijas izmaiņas.
Individuālie indeksi:
![]() - fiziskā apjoma.
- fiziskā apjoma.
![]() - cenu.
- cenu.
![]() - produkcijas vērtības jeb vērtības apjoma.
- produkcijas vērtības jeb vērtības apjoma.
![]() darba algas.
darba algas.
![]() darbinieku skaita.
darbinieku skaita.
Būtībā šie rādītāji ir parasti dinamikas relatīvie lielumi (augšanas tempi).
Kopindeksi (kurus apzīmē ar lielo ![]() ), raksturo saliktu parādību kopējās pārmaiņas. Šajos indeksos izmanto samērotājus. Atkarībā no aprēķināšanas paņēmiena izšķir dažādus to veidus un formas.
), raksturo saliktu parādību kopējās pārmaiņas. Šajos indeksos izmanto samērotājus. Atkarībā no aprēķināšanas paņēmiena izšķir dažādus to veidus un formas.
9.2. Agregātindeksi un vidējie indeksi
Jebkura indeksa galvenā forma ir agregātindeksa forma. Tas veidojas divu absolūto lielumu (agregātu) pretstatīšanas rezultātā.
Produkcijas vērtības (preču apgrozījuma) kopindekss raksturo preču kopējās vērtības attiecību pārskata periodā pret bāzes periodu ![]() .
.
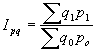 , kur
, kur ![]() - produkcijas vērtība pārskata periodā;
- produkcijas vērtība pārskata periodā; ![]() - produkcijas vērtība bāzes periodā.
- produkcijas vērtība bāzes periodā.
Produkcijas fiziskā apjoma kopindekss ir kvantitatīva rādītāja (produkcijas apjoms) indekss, kur par samērotāju kalpo bāzes perioda cenas. Pēc šī indeksa nosaka fiziskā apjoma pārmaiņu, ja to cenas nebūtu mainījušās: 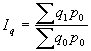 , kur
, kur ![]() - pārskata periodā ražoto preču nosacītā vērtība bāzes perioda cenās.
- pārskata periodā ražoto preču nosacītā vērtība bāzes perioda cenās.
Cenu kopindekss raksturo kā mainās produkcijas vērtība sakarā ar cenu izmaiņām. Par svariem tiek ņemti realizētie preču daudzumi pārskata periodā. Šis ir kvalitatīva rādītāja (cena, pašizmaksa) indekss.
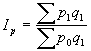 , kur
, kur ![]() - faktiskās produkcijas vērtība pārskata periodā;
- faktiskās produkcijas vērtība pārskata periodā; ![]() - pārskata periodā ražoto preču nosacītā vērtība bāzes perioda cenās.
- pārskata periodā ražoto preču nosacītā vērtība bāzes perioda cenās.
Starp indeksiem pastāv sakarība: ![]()
Agregātindeksus pārveido vidējā indeksa formā, jo ne vienmēr pieejama sākotnējā informācija.
Visvairāk lietotie aritmētiskais vidējais un harmoniskais vidējais indekss.
Aritmētiskais vidējais indekss ir individuālo indeksu svērtais aritmētiskais vidējais. Lai agregātindeksu pārveidotu par aritmētisko vidējo indeksu skaitītājā esošo indeksējamā elementa nozīmi aizstāj ar individuālā indeksa un indeksējamā elementa saucēja reizinājumu.
Cenu kopindekss: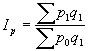 ;
; ![]() ;
; ![]()
Cenu aritmētiskais vidējais indekss: ir 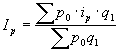
Fiziskā apjoma indekss: 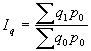 ;
; ![]() ;
; ![]()
Fiziskā apjoma aritmētiskais vidējais indekss: 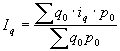
Harmoniskais vidējais indekss ir individuālo indeksu svērtais harmoniskais vidējais.
Cenu un fiziskā apjoma harmoniskie vidējie indeksi būs šādi: 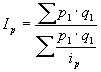 un
un