Mācību materiāls
8. Dinamikas statistiskā izpēte
8.2. Dinamikas rindu vidējie rādītāji
Dinamikas rindu analīzē lieto arī vidējos rādītājus. Dinamikas rindas vidējais līmenis izsaka pētāmās parādības raksturīgo lielumu zināmā laika periodā. Dinamikas rindas vidējo līmeni sauc par hronoloģisko vidējo.
Dinamikas rindu vidējie lielumi raksturo dinamikas rindas īpašības visā aplūkojamā periodā. Lai aprēķinātu dinamikas rindas vidējos lielumus, jāpanāk vispārināmo vienību kopuma viendabīgums un pietiekams skaits.
Intervāla dinamikas rindai vidējo līmeni aprēķina kā vienkāršo aritmētisko vidējo: 
; kur 
dinamikas rindas vidējais līmenis; 
dinamikas rindas līmeņi; 
dinamikas rindu locekļu (līmeņu) skaits.
Intervāla dinamikas rindas ar vienāda ilguma laika periodiem – vidējo līmeni aprēķina pēc nesvērtā aritmētiskā vidējā: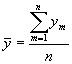 
; kur 
dinamikas rindas vidējais līmenis; 
jebkurš dinamikas rindas līmenis; 
rindas līmeņu (momentu) skaits; 
pirmais dinamikas rindas līmenis.
Intervāla dinamikas rindas ar dažāda ilguma laika periodiem – vidējo līmeni aprēķina pēc svērtā aritmētiskā vidējā: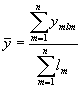 
; kur 
jebkurš dinamikas rindas līmenis; 
rindas līmeņu skaits; 
laika periods, kurā līmenis 
ir nemainīgs; 
pirmais dinamikas rindas līmenis.
Momenta dinamikas rindas ar vienāda ilguma laika periodiem vidējo līmeni aprēķina pēc hronoloģiskā vidējā: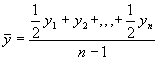 
, kur 
līmeņu (momentu) skaits.
Momenta dinamikas rindas ar dažāda ilguma laika periodiem – vidējo līmeni aprēķina pēc svērtā hronoloģiskā vidējā: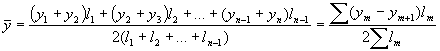 
; kur 
dinamikas rindas līmeņi; 
laika periods, kurā līmenis ir nemainīgs.
Dinamikas rindas vidējo līmeni var arī aprēķināt kā vidējo no vidējiem lielumiem: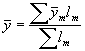 
Vidējais absolūtais pieaugums 
ir pētāmās parādības pārmaiņas ātruma apkopojošs rādītājs laika vienībā. Tas izsaka, par kādu absolūtu lielumu vidēji laika vienībā pieaugusi vai samazinājusies pētāmā parādība visā ar dinamikas rindu aptvertajā periodā. Vidējo absolūto pieaugumu aprēķina kā nesvērto aritmētisko vidējo lielumu: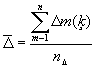 
; kur 
absolūto pieaugumu skaits; 
ķēdes absolūto pieaugumu summa.
Ja zināmi dati par pirmo un pēdējo līmeni, tad vidējo absolūto pieaugumu aprēķina: 
, kur 
absolūto pieaugumu skaits.
Vidējais augšanas temps 
dinamikas rindas līmeņu izmaiņu intensitātes raksturotājs, tas raksturo pētāmās parādības attīstības vidējo intensitāti, rādot, cik reizes vidēji laika vienībā izmainījušies dinamikas rindas līmeņi. Vidējo augšanas tempu var aprēķināt pēc ģeometriskā vidējā formulas: 
; kur 
ķēdes augšanas tempu skaits.
Vidējā pieauguma temps 
rāda, par cik % vidēji palielinājies vai samazinājies pētāmās parādības līmenis visā pētāmajā periodā: 
.