STAT001 Ievads statistikā

Pētot savstarpējās sakarības, statistika risina divus uzdevumus:

1.  nosaka sakarību esamību, konstatē to raksturu, izmantojot kādu no metodēm: grafisko metodi, paralēlo rindu metodi, analītisko grupēšanu vai veicot korelācijas un regresijas analīzi;

2.  nosaka savstarpējo sakarību ciešumu un veic to skaitlisko raksturojumu, izmantojot korelācijas un regresijas analīzi.

Grafisko metodi izmanto, lai noteiktu sakarības raksturu un formu. Grafiskajā tīkliņā ar punktiem iezīmē pētāmā kopuma vienības. No punktu izvietojuma koordinātu sistēmā var spriest par sakarību starp pētāmajām pazīmēm.

Paralēlo rindu metodes būtība ir tāda, ka to izmantojot, salīdzina savā starpā divas vai vairākas variējošu rādītāju rindas, starp kurām loģiski iespējama sakarība.Ja pazīmes pārmaiņām atbilst rezultatīvās pazīmes pārmaiņas, tad var uzskatīt, ka starp šīm pazīmēm pastāv sakarība.

Analītiskās grupēšanas gadījumā kopuma vienības sadala grupās pēc faktoriālās pazīmes. Katrā grupā jāaprēķina rezultatīvās pazīmes vidējās vērtības un tās jāsalīdzina. Rezultātus attēlo grafiski, izdarot secinājumu par sakarībām.

Sakarības ciešuma noteikšanai izmanto korelācijas un regresijas metodi.

Par korelāciju un regresiju analīzi sauc metožu kopumu, ar kuru palīdzību pēta kvantitatīvās sakarības starp mainīgajiem lielumiem, ja tās ir korelatīvas.

Lai izvēlētos pareizo formulu korelatīvas sakarības ciešuma noteikšanai, vispirms jānoskaidro mainīgo lielumu attiecību veids starp mainīgajiem.

Apskatīsim sakarību starp diviem mainīgajiem.

Ja abi mainīgie ir izteikti kvantitatīvi, tad sakarību ciešuma novērtēšanai lieto Pirsona korelācijas koeficientu: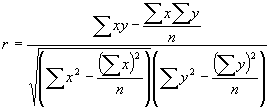

Statistikā lieto vēl citus koeficientus. Rezultāti būs atšķirīgi, kas izskaidrojams tādejādi, ka koeficientu aprēķināšanā lieto pazīmes vērtību dažādas izteiksmes.

Regresijas vienādojums ir matemātiskais modelis sakarībai starp korelatīvi saistītajiem mainīgajiem lielumiem.

Īsā laika posmā lielāko daļu sakarību var uztvert kā lineāras sakarības, tādēļ visbiežāk aprēķinu vienkāršošanai pētījuma sākumā izmanto lineāro funkciju: , kur  neatkarīgais mainīgais lielums jeb faktoriālā pazīme;  atkarīgais mainīgais lielums jeb rezultatīvā pazīme;  regresijas brīvais loceklis, kas parāda aptuveno lielumu, kāds raksturīgs atkarīgajam lielumam bez faktoriālās pazīmes ietekmes;  regresijas sakarības skaitliskā vērtība, kas norāda proporciju, kādā mainīsies rezultatīvā pazīme, mainoties faktoriālajai pazīmei par vienu vienību. Normālvienādojumu sistēmas atrisināšanai jāizskaitļo šādas formulas:

; .

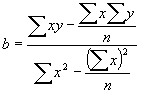Aprēķinātais regresijas vienādojums būs piemērots konkrētam pētījumam, ja tā vidējā standartkļūda būs mazāka par rezultatīvās pazīmes vidējo kvadrātisko nozīmi.

Aprēķinot determinācijas koeficientu, t.i. kāpinot kvadrātā aprēķināto korelācijas koeficientu, un to izsakot procentos, var iegūt pētāmās pazīmes procentuālo daļu, kura atkarīga no faktoriālās pazīmes.