STAT001 Ievads statistikā

Sabiedrisko parādību vispārinošai raksturošanai statistikā izmanto arī t.s. struktūras vidējos. Struktūras vidējie ir konkrētas variantes, kas pētāmās parādības tipisko līmeni izsaka ar kaut kādā ziņā zīmīgu stāvokli sadalījuma rindā.

Moda – variante, kurai sadalījuma rindā ir vislielākais biežums jeb svars.

Modu lieto tad, ja svarīgi izdalīt variantu, kurš sastopams visbiežāk. Modu neietekmē sadalījuma rindas ekstrēmās vērtības. Šo rādītāju izmanto, lai aprakstītu pētāmo parādību, jo rādītājam ir tieksme variēt, salīdzinot vienu izlasi ar otru.

Piemērs. Uzņēmējam svarīgi zināt, kāds ir vispieprasītākais apavu numurs. Ja zināms, ka visvairāk pērk 41 izmēra apavus, tas arī būs modālais lielums. 

Diskrētā rindā moda nav jāaprēķina, bet jānolasa variante ar vislielāko biežumu.

Intervālu sadalījuma rindā modālā lieluma noteikšanai izmanto formulu: , kur  moda;  modālā intervāla zemākā robeža;  modālā intervāla plašums (garums);  modālā intervāla biežums;  pirmsmodālā intervāla biežums;  pēcmodālā intervāla biežums.

Intervālu rindā vispirms jānosaka modālais intervāls. Tas ir intervāls ar vislielāko biežumu sadalījuma rindā. Jo šaurāki intervāli, jo precīzāka moda. Moda būs modālā intervāla centrālais variants.

Mediāna – pazīmes skaitliskā vērtība, kāda tā ir ranžētas sadalījuma rindas vidū esošai vienībai. Pie tam sadalījuma rindu var ranžēt gan augoši, gan dilstoši. Tā attēlo vidējo vērtību, kur variāciju rinda ir sadalīta divās līdzīgās daļās, kur 50% no visām pazīmēm ir vienā pusē, bet otras 50% otrā pusē.

Diskrētā sadalījuma rindā mediānu, t.i. centrālo rādītāju, aprēķina, nosakot tās kārtas numuru: , kur gadījumu skaits.

Intervālu sadalījuma rindai mediānas noteikšanai izmanto formulu: 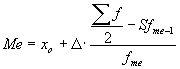, kur  mediāna;  mediānas intervāla plašums (garums);  mediānas intervāla zemākā robeža;  sadalījuma rindas locekļu summa;  pirmsmediānas intervāla uzkrātais biežums;  mediānas intervāla biežums.

Mediānais intervāls – intervāls ranžētā sadalījuma rindā, kurā atrodas kopuma mediānā vienība.

Mediānu neietekmē sadalījuma rindas gan ekstrēmas, gan galējās vērtības, tāpēc mediānu lieto vērtējoša priekšstata iegūšanai gadījumos, ja pētāmās pazīmes vērtībām ir krasas atšķirības.

Mediānas aprēķināšana.

Attēlo vidējo vērtību, kur variāciju rinda ir sadalīta divās līdzīgās daļās. 50% no visām pazīmēm ir vienā daļas pusē, bet otras 50% otrā daļas pusē.

5.3.1. Pratiskais darbs ar atbildi. Mediānas aprēķināšana un modas aprēķināsana.

Lai iegūtu mediānu sarindojam pazīmju rindu pēc lieluma sākot no mazākās 200 €, līdz lielākai, 7000 €. Tālāk vienkārši sadalām iegūto variāciju rindu, kur vienā pusē ir 5 pazīmes, otrā pusē otras 5.

5.3.1. tabula. Ranžēta datu kopas rinda.

Pazīmes nr.	Ienākumi, €	Pazīmes nr.	Ienākumi, €
7.	200	6.	700
1.	400	4.	800
8.	400	9.	1000
2.	500	5.	1200
3.	700	10.	7000

 

No tabulas redzam, ka ranžētas sadalījuma rindas viduspunkts ir 700 € (pazīmes nr. 3. un 6.).

Šajā gadījumā mums abas vidējā punkta pazīmes ir vienādas 700 €. Gadījumā, ja viduspunkta vienas puses pazīme ir lielāka par otras puses pazīmi, mēs abas šīs pazīmes summējam un dalām ar 2.

Piemēram, ja pazīme nr. 3 ir 600 € (nevis kā tabulā 700 €), mediāna ir 650 €.

Tādejādi, mediāna mums atrisina jautājumu un dod precīzu variāciju rindas vidējā aprēķinu, gadījumā, ja mūsu variāciju rindā ir ekstrāmas vērtības.

 

Modas aprēķināšana.

Dotajā piemērā redzam, ka atribūts "ienākumi" parādās visbiežāk divos gadījumos, kad tas ir 400 € (pazīmes 1. un 8.) un 700 € (pazīmes 3. un 6.), skat. 5.3.1. tabulu. No kā izriet, ka dotajā datu kopā ir 2 modas, - 400 €

 un 700 €. Gadījumā, ja 1. pazīmes vērtība ir 300 €, tad datu kopā ir 1 moda, 700 €.

Tātad šis lielums mums reprezentē ienākuma modālo vērtību, vai teiksim, vistipiskāko vērtību.