STAT001 Ievads statistikā

Statistiskie vidējie lielumi ir vispārinoši rādītāji, kas izsaka masveida parādību tipiskos, raksturīgos līmeņus un stāvokļus konkrētos vietas un laika apstākļos.

Tātad vidējais lielums raksturo to centrālo tendenci, dod iespēju salīdzināt dažādus kopumus, objektus. Tos lieto arī dinamikas pētījumos un statistiski nosakot sakarības starp parādībām.

Vidējā lieluma īpašības:

• vidējais lielums vienmēr ir daudzu lielumu vidējais;
  
• vidējā lielumā izpaužas lielā skaita likuma darbība - sedzas nejaušo faktoru izsaukto skaitlisko vērtību novirzes un izpaužas būtisko faktoru izsauktās tipiskās, raksturīgās vērtības;
  
• vidējos lielumus rēķina kvalitatīvi viendabīgam kopumam;
  
• vidējais lielums ir daudzu un dažādu individuālo viena un tā pašā veida lielumu vidējais lielums.
  

Pastāv divu veidu vidējie lielumi:

• pakāpju vidējie;
• struktūras vidējie.

Pakāpju vidējie rādītāji ir:

• aritmētiskais vidējais;
• ģeometriskais vidējais;
• kvadrātiskais vidējais;
• harmoniskais vidējais u.c.

Struktūras vidējie rādītāji ir:

• moda;
• mediāna;
• kvartile.

Kā jau tika minēts, statistikā lieto vairākus vidējo lielumu veidus, kas atšķiras pēc aprēķināšanas metodēm un saistās ar aprēķināto rādītāju sabiedriski ekonomisko būtību.

Vidējie lielumi

Pakāpju vidējie lielumi – visizplatītākais ir vienkāršais aritmētiskais vidējais, ko aprēķina pēc formulas: 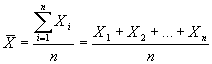, kur aritmētiskais vidējais; variante; kopas vienību skaits.

Ģeometriskais vidējais – to galvenokārt lieto dinamikas analīzē, raksturo pētāmās parādības vidējo attīstības ātrumu (vidējo augšanas tempu). Aprēķina pēc formulas: , kur ģeometriskais vidējais; dinamikas rindas līmeņu skaits; dinamikas rindas līmeņi (augšanas tempi).

Vidējā ģeometriskā aprēķināšanas piemērs (nosacīti dati): 

5.1.1.tabula. Uzņēmuma A eksports no 2012.gada līdz 2016.gadam, tūkst. EUR

Gadi	2012	2013	2014	2015	2016
Eksports	15 634	25 867	37 450	27 889	17 278

Secinājums. Eksports katru gadu vidēji palielinājies par 28%.

Kvadrātiskais vidējais – to izmanto tad, ja dati, kuru vidējais jāatrod, ir radušies, rēķinot novirzes no kāda cita vidējā. Šo vidējo lieto sadalījuma rindas pazīmes individuālo nozīmju variāciju pētīšanā. Aprēķina pēc formulas: 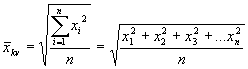, kur kvadrātiskais vidējais; sadalījuma rindas līmeņu skaits; pazīmes vērtība jeb novirze no .

Harmonisko vidējo aprēķina pēc formulas: 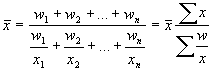, 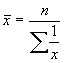kur vidējais; summas zīme; varianti skaits; varianti; varianta un biežuma reizinājums (kopējais).

Vienkāršos aritmētiskos vidējos lieto, aprēķinot vidējos lielumus nesagrupētiem datiem.

Sociālekonomiskajos aprēķinos harmoniskā vidējā lietošana nepieciešama tad, ja nav tiešas sākotnējās informācijas, kas būtu piemērota aritmētiskā vidējā aprēķināšanai.

5.1.1. Praktiskais darbs ar atbildi. Vidējā aritmētiskās aprēķināšana.

Ir atlasīti pieci uzņēmumi, n=5, kuros strādā šāds darbinieku skaits 46, 54, 42, 46, 32.

x₁ = 46    x₂ = 54     x₃ = 42    x₄ = 46     x₅ = 32      

Tātad summējot iegūstam kopējo darbinieku skaitu 220, ko izdalām ar 5. Tātad vidējais darbinieku skaits ir 44.

5.1.2. Praktiskais darbs ar atbildi. Vidējā aritmētiskās aprēķināšana.

Pieņemsim, ka doti 10 darbinieku ienākumi, EUR (noapaļoti līdz tuvākajam simtam).

5.1.2. tabula. Sākotnējie dati.

Pazīmes nr.	Ienākumi, EUR	Pazīmes nr.	Ienākumi, EUR
1.	400	6.	700
2.	500	7.	200
3.	700	8.	400
4.	800	9.	1000
5.	1200	10.	700

 Lai aprēķinātu vidējo aritmētisko, summējam visu darbinieku ienākumus kopā. Iegūstam 6600 €, tad dalām ar kopējo pazīmju skaitu (n = 10), iegūstam vidējo aritmētisko 660 €.

 Vidējā aritmētiskā īpašība ir, ka mainoties jebkuras pazīmes absolūtajai vērtībai, mainās arī vidējā aritmētiskās vērtība. Varam teikt, ka vidējais aritmētiskais ir ļoti "demokrātisks” rādītājs.

 

Gadījumos, kad variāciju rindā ir viena vai divas ekstrēmas vērtības vidējais aritmētiskais, kā variāciju rindas novērtējuma rādītājs mums nederēs.

Piemērs. Pieņemsim, ka pazīmei nr. 10 vērtība ir nevis 700, bet 7000 EUR.

 5.1.3. tabula. Dati ar ekstrēmu vērtību

Pazīmes nr.	Ienākumi, EUR	Pazīmes nr.	Ienākumi, EUR
1.	400	6.	700
2.	500	7.	200
3.	700	8.	400
4.	800	9.	1000
5.	1200	10.	7000

 

Iegūstam, ka kopējie darbinieku ienākumi ir 12 900 €, bet vidējais aritmētiskais ir 1290 €. Deviņas no desmit pazīmēm ir mazākas par iegūto skaitli. Tas ir netipisks vidējais.