Mācību materiāls
5. Centrālās tendences rādītāji
5.4. Variācijas statistiskā analīze
Statistiskā kopuma raksturošanai nepietiek tikai ar vidējo lielumu, jo tajā izzūd pētāmās parādības atsevišķo vienību svārstības jeb variācijas.
Variācija – jebkuras statistiskās kopas īpašība- pazīmes skaitlisko un atributīvo nozīmju individuālā atšķirība, kuru izraisa dažādu faktoru ietekme. Mērīt variāciju nozīmē noteikt kopas vienību skaitlisko vērtību tuvības vai atšķirības pakāpi. Jo mazāka variācija, jo tipiskāks ir vidējais lielums un viendabīgāks kopums. Jo vairāk novirzās pazīmes individuālās vērtības no kopuma vidējā, jo netipiskāks ir vidējais lielums.
Variācijas mērīšanai statistikā izmanto vairākus variācijas rādītājus. Svarīgākie no tiem ir:
- variācijas apjoms jeb amplitūda;
- vidējā lineārā novirze;
- standartnovirze jeb vidējā kvadrātiskā novirze;
- dispersija;
- variācijas koeficients.
Variācijas apjoms ir starpība starp pazīmes lielāko un mazāko vērtību. 
, kur 
variācijas apjoms jeb amplitūda; 
pazīmes lielākā vērtība; 
pazīmes mazākā vērtība. [1]
Vidējā lineārā novirze 
(alfa) ir aritmētiskais vidējais noatsevišķu varianšu absolūto noviržu no aritmētiskā vidējā.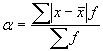 
, kur 
vidējā lineārā novirze; 
variantes biežums; 
kopas vienību skaits; 
grupas vidējā vērtība; 
pazīmes aritmētiskais vidējais. [2]
Dispersija 
ir atsevišķu varianšu noviržu no aritmētiskā vidējā kvadrātu vidējais lielums.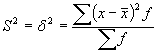 
, kur 
dispersija; 
variantes biežums; 
kopas vienību skaits; 
grupas vidējā vērtība (rindas gadījumā – intervāla vidējā nozīme); 
pazīmes aritmētiskais vidējais.
Apzīmējumu 
lieto, ja dispersiju rēķina izlases datiem. [3]
Standartnovirze jeb vidējā kvadrātiskā novirze – ir visizplatītākais variācijas rādītājs. Tā ir kvadrātsakne no dispersijas un parāda, kā izvietojas vienību galvenā masa attiecībā pret vidējo.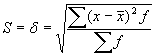 
, kur 
dispersija; 
variantes biežums; 
kopas vienību skaits; 
grupas vidējā vērtība; 
pazīmes aritmētiskais vidējais. [4]
Ja pētījumā izšķiroša nozīme ir relatīvās variācijas novērtēšanai, jālieto relatīvās variācijas rādītāji, variācijas koeficients, kurš izsaka variācijas salīdzinošu pakāpi. To izsaka procentos. Ja variācijas koeficients nepārsniedz 33 %, tad statistiskais kopums ir viendabīgs. Aprēķina formula:
, kur 
variācijas koeficients; 
grupas vidējā vērtība.
5.4.1. Praktiskais darbs ar atbildi. Dispersijas un standartnovirzes aprēķins.
Dota izlases, n= 17 datu kopa:
| 32.2 |
29.5 |
29.9 |
32.4 |
30.5 |
30.1 |
32.1 |
35.2 |
10.0 |
20.6 |
28.6 |
30.5 |
38.0 |
33.0 |
29.4 |
37.1 |
28.6 |
|---|
Arēķināt vidējo aritmētisko, dispersiju un standartnovirzi.
Aprēķinot izmantojam [4] vienādojumu.
Vidējais aritmētiskais = 29.86
Dispersija, S2 = (32.2 - 29.86)2 + (29.5 - 29.86)2 + (29.9 - 29.86)2 + (29.9 - 29.86)2 + ....+ (28.6 - 29.86)2 / 17 -1 = 658.5592 / 16 = 41.15995
Standartnovirze, S = \( \sqrt[]{41.15995} \) = 6.42